题目内容
已知椭圆C的方程是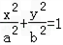 (a>b>0),点A,B分别是椭圆的长轴的左、右端点,左焦点坐标为(﹣4,0),且过点
(a>b>0),点A,B分别是椭圆的长轴的左、右端点,左焦点坐标为(﹣4,0),且过点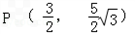 .
.
(Ⅰ)求椭圆C的方程;
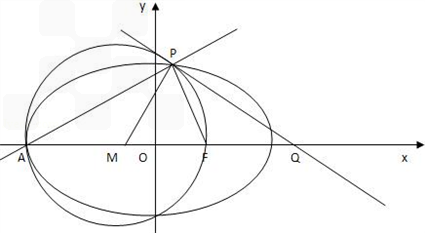
(Ⅱ)已知F是椭圆C的右焦点,以AF为直径的圆记为圆M,试问:过P点能否引圆M的切线,若能,求出这条切线与x轴及圆M的弦PF所对的劣弧围成的图形的面积;若不能,说明理由.
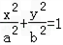 (a>b>0),点A,B分别是椭圆的长轴的左、右端点,左焦点坐标为(﹣4,0),且过点
(a>b>0),点A,B分别是椭圆的长轴的左、右端点,左焦点坐标为(﹣4,0),且过点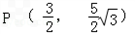 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)已知F是椭圆C的右焦点,以AF为直径的圆记为圆M,试问:过P点能否引圆M的切线,若能,求出这条切线与x轴及圆M的弦PF所对的劣弧围成的图形的面积;若不能,说明理由.

解:(Ⅰ)因为椭圆C的方程为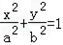 ,(a>b>0),
,(a>b>0),
∴a2=b2+16,即椭圆的方程为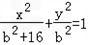 ,
,
∵点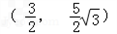 在椭圆上,
在椭圆上,
∴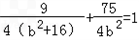 ,解得b2=20或b2=﹣15(舍),
,解得b2=20或b2=﹣15(舍),
由此得a2=36,
所以,所求椭圆C的标准方程为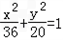 .
.
(Ⅱ)由(Ⅰ)知A(﹣6,0),F(4,0),
又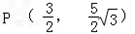 ,则得
,则得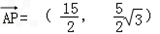 ,
,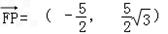
所以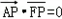 ,即∠APF=90°,
,即∠APF=90°,
△APF是Rt△,所以,以AF为直径的圆M必过点P,
因此,过P点能引出该圆M的切线,
设切线为PQ,交x轴于Q点,
又AF的中点为M(﹣1,0),则显然PQ⊥PM,
而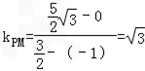 ,所以PQ的斜率为
,所以PQ的斜率为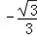 ,
,
因此,过P点引圆M的切线方程为: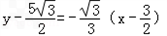 ,即
,即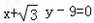
令y=0,则x=9,∴Q(9,0),又M(﹣1,0),
所以 ,
,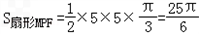
因此,所求的图形面积是S=S△PQM﹣S扇形MPF=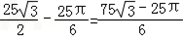 .
.
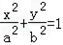 ,(a>b>0),
,(a>b>0),∴a2=b2+16,即椭圆的方程为
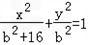 ,
,∵点
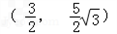 在椭圆上,
在椭圆上,∴
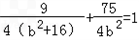 ,解得b2=20或b2=﹣15(舍),
,解得b2=20或b2=﹣15(舍),由此得a2=36,
所以,所求椭圆C的标准方程为
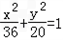 .
.(Ⅱ)由(Ⅰ)知A(﹣6,0),F(4,0),
又
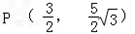 ,则得
,则得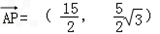 ,
,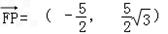
所以
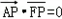 ,即∠APF=90°,
,即∠APF=90°,△APF是Rt△,所以,以AF为直径的圆M必过点P,
因此,过P点能引出该圆M的切线,
设切线为PQ,交x轴于Q点,
又AF的中点为M(﹣1,0),则显然PQ⊥PM,
而
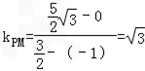 ,所以PQ的斜率为
,所以PQ的斜率为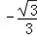 ,
,因此,过P点引圆M的切线方程为:
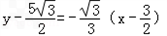 ,即
,即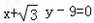
令y=0,则x=9,∴Q(9,0),又M(﹣1,0),
所以
 ,
,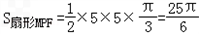
因此,所求的图形面积是S=S△PQM﹣S扇形MPF=
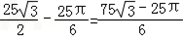 .
.

练习册系列答案
相关题目
 (1)求右焦点坐标是(2,0),且经过点(-2,-
(1)求右焦点坐标是(2,0),且经过点(-2,-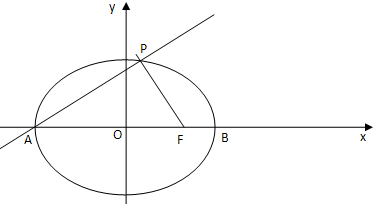 已知椭圆C的方程是
已知椭圆C的方程是 (I)已知椭圆C的方程是
(I)已知椭圆C的方程是