题目内容
(1)求右焦点坐标是(2,0),且经过点( -2 , -| 2 |
(2)已知椭圆C的方程是
| x2 |
| a2 |
| y2 |
| b2 |
分析:(1)求椭圆的方程关键是计算a2与b2的值,由焦点F(2,0)且经过点( -2 , -
)的椭圆的标准方程,构造方程组,解方程组即可求出a2与b2的值,代入即可得到椭圆的标准方程.
(2)本题的解答要用到“设而不求”的思想,即设出直线与椭圆两交点的坐标,然后将直线方程代入椭圆的方程,利用韦达定理找出点横、纵坐标和与积的关系,代入验证.
| 2 |
(2)本题的解答要用到“设而不求”的思想,即设出直线与椭圆两交点的坐标,然后将直线方程代入椭圆的方程,利用韦达定理找出点横、纵坐标和与积的关系,代入验证.
解答:解:(1)设椭圆的标准方程为
+
=1,a>b>0,
所以a2=b2+4,即椭圆的方程为
+
=1,
又点(-2,-
)在椭圆上,所以
+
=1,
解得b2=4或b2=-2(舍),
由此得a2=8,即椭圆的标准方程为
+
=1.、
(2)设直线l的方程为y=kx+m,与椭圆C的交点A(x1,y1)、B(x2,y2),
则有
,
解得(b2+a2k2)x2+2a2kmx+a2m2-a2b2=0,△>0,所以m2<b2+a2k2,即-
<m<
.
则x1+x2=-
,y1+y2=kx1+m+kx2+m=
,
所以AB中点M的坐标为(-
,
).
所以线段AB的中点M在过原点的直线b2x+a2ky=0上.
| x2 |
| a2 |
| y2 |
| b2 |
所以a2=b2+4,即椭圆的方程为
| x2 |
| b2+4 |
| y2 |
| b2 |
又点(-2,-
| 2 |
| 4 |
| b2+4 |
| 2 |
| b2 |
解得b2=4或b2=-2(舍),
由此得a2=8,即椭圆的标准方程为
| x2 |
| 8 |
| y2 |
| 4 |
(2)设直线l的方程为y=kx+m,与椭圆C的交点A(x1,y1)、B(x2,y2),
则有
|
解得(b2+a2k2)x2+2a2kmx+a2m2-a2b2=0,△>0,所以m2<b2+a2k2,即-
| b2+a2k2 |
| b2+a2k2 |
则x1+x2=-
| 2a2km |
| b2+a2k2 |
| 2b2m |
| b2+a2k2 |
所以AB中点M的坐标为(-
| a2km |
| b2+a2k2 |
| b2m |
| b2+a2k2 |
所以线段AB的中点M在过原点的直线b2x+a2ky=0上.
点评:运用待定系数法求椭圆标准方程,即设法建立关于a,b的方程组,先定型、再定量,若位置不确定时,
考虑是否两解,有时为了解题需要,椭圆方程可设为mx2+ny2=1(m>0,n>0,m≠n),由题目所给条件求出m,n即可.
也可根据条件构造方程(组)解方程(组)给出a2与b2的值,代入即可得到椭圆的标准方程.
考虑是否两解,有时为了解题需要,椭圆方程可设为mx2+ny2=1(m>0,n>0,m≠n),由题目所给条件求出m,n即可.
也可根据条件构造方程(组)解方程(组)给出a2与b2的值,代入即可得到椭圆的标准方程.

练习册系列答案
相关题目
 (1)求右焦点坐标是(2,0),且经过点(-2,-
(1)求右焦点坐标是(2,0),且经过点(-2,- 的椭圆的标准方程;
的椭圆的标准方程; 有共同的焦点并且与双曲线
有共同的焦点并且与双曲线 有共同渐近线的双曲线方程.
有共同渐近线的双曲线方程.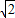 )的椭圆的标准方程.
)的椭圆的标准方程. +
+ =1(a>b>0).设斜率为k的直线l交椭圆C于A、B两点,AB的中点为M.证明:当直线l平行移动时,动点M在一条过原点的定直线上.
=1(a>b>0).设斜率为k的直线l交椭圆C于A、B两点,AB的中点为M.证明:当直线l平行移动时,动点M在一条过原点的定直线上.