题目内容
如图，在半径为R的⊙O中，弦AB的长与半径R相等，C是优弧  | AB |
分析：连接OA、OB，由于弦AB的长和半径相等，可证得△AOB是等边三角形，即∠AOB=60°，再由同弧所对的圆周角和圆心角的关系可求得∠ACB的度数．
解答：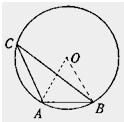
解：连接OA、OB；
∵OA=OB=AB=R，
∴△OAB是等边三角形；
∴∠AOB=60°；
∴∠ACB=
∠AOB=30°．
故答案为：30．
解：连接OA、OB；∵OA=OB=AB=R，
∴△OAB是等边三角形；
∴∠AOB=60°；
∴∠ACB=
| 1 |
| 2 |
故答案为：30．
点评：此题主要考查的是圆周角定理：同弧所对的圆周角是圆心角的一半．属于基础题．
练习册系列答案
天天向上口算本系列答案
相关题目
如图，在半径为r的圆内作内接正六边形，再作正六边形的内切圆，又在此内切圆内作内接正六边形，如此无限继续下去，设Sn为前n个圆的面积之和，则| lim |
| n→∞ |
| A、2πr2 | ||
B、
| ||
| C、4πr2 | ||
| D、6πr2 |
如图，在半径为R的圆内随机撒一粒黄豆，它落在阴影部分内接正三角形上的概率是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在半径为r的圆内作内接正六边形，再作正六边形的内切圆，又在此内切圆内作内接正六边形，如此无限继续下去，设Sn为前n个正六边形的面积之和，则
内切圆，又在此内切圆内作内接正六边形，如此无限继续下
为前n个圆的面积之和，则
=
B．
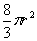
D．