题目内容
已知三角形ABC的面积S=
,则∠C的大小是( )
| a2+b2-c2 |
| 4 |
分析:根据正弦定理的面积公式和余弦定理,化简题中等式可得
absinC=
abcosC,得sinC=cosC,结合三角形内角的范围,即可求出∠C的大小.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:根据正弦定理的面积公式,得
△ABC的面积S=
absinC
∵S=
,
∴
absinC=
又∵a2+b2-c2=2abcosC
∴
absinC=
abcosC,得sinC=cosC
∵C∈(0,π),∴C=
,即C=45°
故选:A
△ABC的面积S=
| 1 |
| 2 |
∵S=
| a2+b2-c2 |
| 4 |
∴
| 1 |
| 2 |
| a2+b2-c2 |
| 4 |
又∵a2+b2-c2=2abcosC
∴
| 1 |
| 2 |
| 1 |
| 2 |
∵C∈(0,π),∴C=
| π |
| 4 |
故选:A
点评:本题给出三角形面积关于边的式子,求角C的大小.着重考查了三角形的面积公式、正余弦定理和特殊角的三角函数值等知识,属于基础题.

练习册系列答案
相关题目
 如图,已知四面体ABCD的四个面均为锐角三角形,EFGH分别是边AB,BC,CD,DA上的点,BD||平面EFGH,且EH=FG.
如图,已知四面体ABCD的四个面均为锐角三角形,EFGH分别是边AB,BC,CD,DA上的点,BD||平面EFGH,且EH=FG.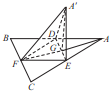 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题: ),顶点C在
),顶点C在 轴
轴 与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面
与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面