题目内容
(2007
上海,20)如果有穷数列 ,
,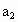 ,
, ,…,
,…, (n为正整数)满足条件
(n为正整数)满足条件 即
即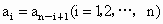 ,我们称其为“对称数列”.例如,由组合数组成的数列
,我们称其为“对称数列”.例如,由组合数组成的数列 就是“对称数列”.
就是“对称数列”.
(1)
设 是项数为7的“对称数列”,其中
是项数为7的“对称数列”,其中 是等差数列,且
是等差数列,且 .依次写出
.依次写出 的每一项;
的每一项;
(2)
设 是项数为2k-1(正整数k>1)的“对称数列”,且
是项数为2k-1(正整数k>1)的“对称数列”,且 ,
, ,…,
,…,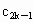 是首项为50,公差为-4的等差数列.记
是首项为50,公差为-4的等差数列.记 各项的和为
各项的和为 .当k为何值时,
.当k为何值时, 取得最大值?并求出
取得最大值?并求出 的最大值;
的最大值;
(3)
对于确定的正整数m>1,写出所有项数不超过2m的“对称数列”,使得 依次是该数列中连续的项;当m>1500时,求其中一个“对称数列”前2008项的和
依次是该数列中连续的项;当m>1500时,求其中一个“对称数列”前2008项的和 .
.
答案:略
解析:
解析:
|
解析: (1)设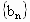 的公差为d, 的公差为d,
则 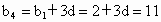 ,解得d=3, ,解得d=3,
∴数列 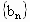 为2,5,8,11,8,5,2. 为2,5,8,11,8,5,2.
(2)
∴当 k=13时,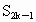 取得最大值. 取得最大值.
(3) 所有可能的“对称数列”是:
当 1500<m≤2007时,
对于②,当 m≥2008时,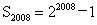 . .
当 1500<m≤2007时,
对于③,当 m≥2008时,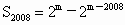 , ,
当 1500<m≤2007时,
对于④,当 m≥2008时,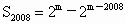 . .
当 1500<m≤2007时,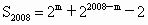 . . |

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
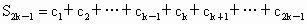
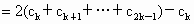
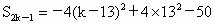
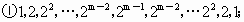
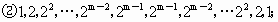
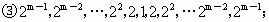
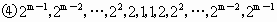
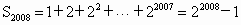

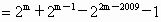
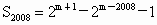
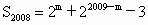
 ;
;
