题目内容
下列推理过程，错误的是 ．
①l∥α，A∈l⇒A∉α；
②A∈l，A∈α，B∈l⇒B∈α；
③A∈α，A∈β，B∈α，B∈β⇒α∩β=AB；
④A，B，C∈α，A，B，C∈β，并且A，B，C不共线⇒α=β．
①l∥α，A∈l⇒A∉α；
②A∈l，A∈α，B∈l⇒B∈α；
③A∈α，A∈β，B∈α，B∈β⇒α∩β=AB；
④A，B，C∈α，A，B，C∈β，并且A，B，C不共线⇒α=β．
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：利用空间中点、线、面间的关系求解．
解答：
解：①l∥α，A∈l，由直线与平面平行的性质得A∉α，故①正确；
②A∈l，A∈α，B∈l，则点B不一定在平面α内，故②错误；
③A∈α，A∈β，B∈α，B∈β，则由公理二得α∩β=AB，故③正确；
④A，B，C∈α，A，B，C∈β，并且A，B，C不共线，则由平面的性质得α=β，故④正确．
故答案为：②．
②A∈l，A∈α，B∈l，则点B不一定在平面α内，故②错误；
③A∈α，A∈β，B∈α，B∈β，则由公理二得α∩β=AB，故③正确；
④A，B，C∈α，A，B，C∈β，并且A，B，C不共线，则由平面的性质得α=β，故④正确．
故答案为：②．
点评：本题考查命题真假的判断，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
全程金卷系列答案
相关题目
定义在R上的函数满足f（x）=f（x+2），当x∈[1，3]时，f（x）=2-|x-2|，则（ ）
A、f(sin
| ||||
| B、f （sin1）＞f （cos1） | ||||
C、f(cos
| ||||
| D、f （cos2）＞f （sin2） |
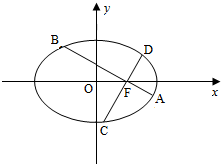如图，在平面直角坐标系xOy中，椭圆