题目内容
正方体ABCD-A1B1C1D1的各个顶点与各棱的中点共20个点中,任取两点连成直线,在
这些直线中任取一条,它与对角线BD1垂直的概率为( )
这些直线中任取一条,它与对角线BD1垂直的概率为( )
A.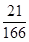 | B.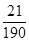 | C.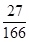 | D.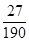 |
C
分析:由题意知本题是一个古典概型,试验发生包含的所有事件是从20个点中取2个,但每条棱上3点任取2个是重复的,满足条件的事件是要与BD1垂直,则应与面A1DC1平行或在其面内,与A1C1平行或重合的有9条,根据古典概型公式得到结果.
解答:解:由题意知本题是一个古典概型,
从20个点中取2个,共
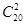 =190,
=190,但每条棱上3点任取2个是重复的,
∴分母为190-12
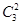 +12=166,
+12=166,要与BD1垂直,则应与面A1DC1平行或在其面内,与A1C1平行或重合的有9条,共27条,
∴P=
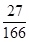 .
.故选C.
点评:古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.

练习册系列答案
相关题目
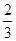
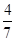
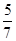
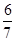
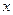
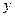
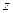
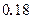 .
.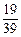 ,求选出的两人性别不同的概率;
,求选出的两人性别不同的概率;