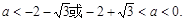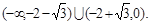题目内容
设(2x-1)5=a0+a1x+a2x2+…+a5x5,求:(1)a0+a1+a2+a03+a4;
(2)|a0|+|a1|+|a2|+|a3|+|a4|+|a5|;
(3)a1+a3+a5;
(4)(a0+a2+a4)2-(a1+a3+a5)2.
解析:设f(x)=(2x-1)5=a0+a1x+a2x2+…+a5x5,则f(1)=a0+a1+a2+…+a5=1,
f(-1)=a0-a1+a2-a3+a4-a5=(-3)5=-243.
(1)∵a5=25=32,∴a0+a1+a2+a3+a4=f(1)-32=-31.
(2)|a0|+|a1|+|a2|+…+|a5|=-a0+a1-a2+a3-a4+a5=-f(-1)=243.
(3)∵f(1)-f(-1)=2(a1+a3+a5),∴a1+a3+a5=![]() =122.
=122.
(4)(a0+a2+a4)2-(a1+a3+a5)2=(a0+a1+a2+a3+a4+a5)(a0-a1+a2-a3+a4-a5)=f(1)×f(-1)=-243.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
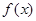 的二次项系数为
的二次项系数为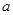 ,且不等式
,且不等式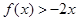 的解集为
的解集为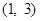 ,
,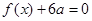 有两个相等的根,求
有两个相等的根,求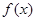 的最大值为正数,求
的最大值为正数,求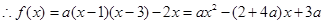 ①
①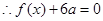
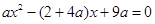 ②
②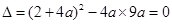 ,
,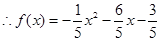
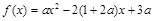
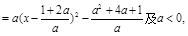
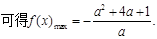
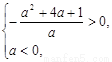 解得:
解得: