题目内容
设x、y是实数,满足(x-1)2+y2=1,当x+| 3 |
分析:写出圆的参数方程,代入x+
y+m≥0,利用三角函数的知识化简,确定m的取值范围.
| 3 |
解答:解:(x-1)2+y2=1,所以x=1+cosθ,y=sinθ,所以m≥-x-
y=-1-cosθ-
sinθ=-2sin(θ+
)-1,因为-2sin(θ+
)-1的最大值为 1;
所以m的取值范围是:m≥1
故答案为:m≥1
| 3 |
| 3 |
| π |
| 6 |
| π |
| 6 |
所以m的取值范围是:m≥1
故答案为:m≥1
点评:本题是基础题,考查圆的参数方程的应用,三角函数的最值,恒成立问题的应用,考查计算能力,好题,常考题型.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 y+m≥0时,则m的取值范围是________.
y+m≥0时,则m的取值范围是________.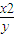 ≤9,则
≤9,则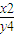 的最大值是 .
的最大值是 .