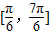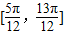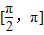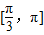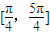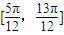题目内容
若方程(x-2cosθ)2+(y-2sinθ)2=1(0≤θ<2π)的任意一组解(x,y)都满足不等式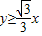 ,则θ的取值范围是( )
,则θ的取值范围是( )A.
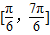
B.
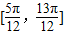
C.
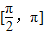
D.
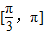
【答案】分析:根据题意,方程(x-2cosθ)2+(y-2sinθ)2=1(0≤θ≤2π)表示的曲线在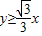 的左上方(包括相切),可建立不等式,利用三角函数知识,即可求得θ的取值范围.
的左上方(包括相切),可建立不等式,利用三角函数知识,即可求得θ的取值范围.
解答:解:由题意,方程(x-2cosθ)2+(y-2sinθ)2=1(0≤θ≤2π)表示的曲线在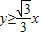 的左上方(包括相切),则
的左上方(包括相切),则
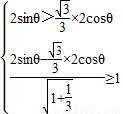 ,∴sin(θ-
,∴sin(θ-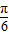 )≥
)≥
∵0≤θ≤2π,∴-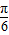 ≤θ-
≤θ- ≤
≤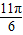
∴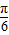 ≤θ-
≤θ-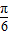 ≤
≤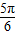
∴θ的取值范围是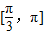
故选D.
点评:本题考查圆的方程,考查三角函数知识的运用,解题的关键是将问题转化为方程(x-2cosθ)2+(y-2sinθ)2=1(0≤θ≤2π)表示的曲线在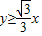 的左上方(包括相切).
的左上方(包括相切).
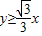 的左上方(包括相切),可建立不等式,利用三角函数知识,即可求得θ的取值范围.
的左上方(包括相切),可建立不等式,利用三角函数知识,即可求得θ的取值范围.解答:解:由题意,方程(x-2cosθ)2+(y-2sinθ)2=1(0≤θ≤2π)表示的曲线在
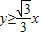 的左上方(包括相切),则
的左上方(包括相切),则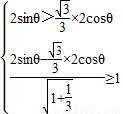 ,∴sin(θ-
,∴sin(θ-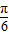 )≥
)≥
∵0≤θ≤2π,∴-
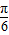 ≤θ-
≤θ- ≤
≤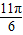
∴
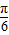 ≤θ-
≤θ-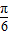 ≤
≤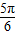
∴θ的取值范围是
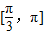
故选D.
点评:本题考查圆的方程,考查三角函数知识的运用,解题的关键是将问题转化为方程(x-2cosθ)2+(y-2sinθ)2=1(0≤θ≤2π)表示的曲线在
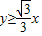 的左上方(包括相切).
的左上方(包括相切). 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
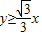 ,则θ的取值范围是( )
,则θ的取值范围是( )