题目内容
对于任意实数x,y,定义: ,如果函数f(x)=x2,g(x)=x,h(x)=-x+2,那么满足F(F(f(x),g(x)),F(g(x),h(x))≥2的x的集合是 .
,如果函数f(x)=x2,g(x)=x,h(x)=-x+2,那么满足F(F(f(x),g(x)),F(g(x),h(x))≥2的x的集合是 .
【答案】分析:先把定义 ,转化为
,转化为 ;再把所求不等式转化即可求出结论.
;再把所求不等式转化即可求出结论.
解答:解:因为: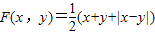 =
= ;
;
∴F(f(x),g(x))= ;
;
F(g(x),h(x))= .
.
而x2=-x+2⇒x=1或x=-2.
∴F(F(f(x),g(x)),F(g(x),h(x))= ;
;
当x≥1或x≤-2时,F(F(f(x),g(x)),F(g(x),h(x))≥2转化为x2≥2⇒x≥ 或x≤-
或x≤- ;
;
故x≥ 或x≤-2;
或x≤-2;
当-2<x<1时,F(F(f(x),g(x)),F(g(x),h(x))≥2转化为:-x+2≥2⇒x≤0,
故-2<x≤0;
综上:F(F(f(x),g(x)),F(g(x),h(x))≥2的解集为:{x|x≤0或x≥ }.
}.
故答案为:{x|x≤0或x≥ }.
}.
点评:本题主要在新定义下考查一元二次不等式的解法.解决本题的关键在于把新定义转化.
 ,转化为
,转化为 ;再把所求不等式转化即可求出结论.
;再把所求不等式转化即可求出结论.解答:解:因为:
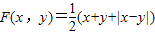 =
= ;
;∴F(f(x),g(x))=
 ;
;F(g(x),h(x))=
 .
.而x2=-x+2⇒x=1或x=-2.
∴F(F(f(x),g(x)),F(g(x),h(x))=
 ;
;当x≥1或x≤-2时,F(F(f(x),g(x)),F(g(x),h(x))≥2转化为x2≥2⇒x≥
 或x≤-
或x≤- ;
;故x≥
 或x≤-2;
或x≤-2;当-2<x<1时,F(F(f(x),g(x)),F(g(x),h(x))≥2转化为:-x+2≥2⇒x≤0,
故-2<x≤0;
综上:F(F(f(x),g(x)),F(g(x),h(x))≥2的解集为:{x|x≤0或x≥
 }.
}.故答案为:{x|x≤0或x≥
 }.
}.点评:本题主要在新定义下考查一元二次不等式的解法.解决本题的关键在于把新定义转化.

练习册系列答案
相关题目