题目内容
.已知数列 是
是 正数组成的数列,其前n项和为
正数组成的数列,其前n项和为 ,对于一切
,对于一切 均有
均有 与2的等差中项等于
与2的等差中项等于 与2的等比中项。
与2的等比中项。
(1)计算 并由此猜想
并由此猜想 的通项公式
的通项公式 ;
;
(2)用数学归纳法证明(1)中你的猜想。
解:(1)由 得
得 可求得
可求得 ,┈5分
,┈5分
由此猜想 的通项公式
的通项公式 。 ┈┈┈7分
。 ┈┈┈7分
(2)证明:①当 时,
时, ,等式成立; ┈┈┈9分
,等式成立; ┈┈┈9分
②假设当 时,等式成立,即
时,等式成立,即 , ┈┈┈11分
, ┈┈┈11分
 当
当 时,等式也成立
时,等式也成立 。 ┈┈┈13分
。 ┈┈┈13分
由①②可得 成立。 ┈┈┈15分
成立。 ┈┈┈15分
解析

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 是正数组成的数列,其前n项和为
是正数组成的数列,其前n项和为 ,对于一切
,对于一切 均有
均有 与2的等差中项等于
与2的等差中项等于 ;并由此猜想
;并由此猜想 是正数组成的数列,其前n项和
是正数组成的数列,其前n项和 为
为 ,对于一切
,对于一切 均有
均有 与2的等差中项等于
与2的等差中项等于 并由此猜想
并由此猜想 是正数组成的数列,其前n项和为
是正数组成的数列,其前n项和为 ,对于一切
,对于一切 均有
均有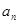 与2的等差中项等于
与2的等差中项等于 ;并由此猜想
;并由此猜想 是正数组成的数列,其前n项和为
是正数组成的数列,其前n项和为 ,对于一切
,对于一切 均有
均有 与2的等差中项等于
与2的等差中项等于 并由此猜想
并由此猜想