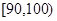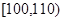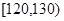题目内容
(本题满分14分)某突发事件,在不采取任何预防措施的情况下发生的概率为 ,一旦发生,将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择,单独采用甲、乙预防措施所需的费用分别为40万元和20万元,采用相应预防措施后此突发事件不发生的概率分别为
,一旦发生,将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择,单独采用甲、乙预防措施所需的费用分别为40万元和20万元,采用相应预防措施后此突发事件不发生的概率分别为 和
和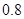 .若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用,请分别计算这几种预防方案的总费用,并指出哪一种预防方案总费用最少.
.若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用,请分别计算这几种预防方案的总费用,并指出哪一种预防方案总费用最少.
(注:总费用 = 采取预防措施的费用+发生突发事件损失的期望值)
(1)不采取预防措施时,总费用即损失期望值为 (万元)
. …………2分
(万元)
. …………2分
(2)若单独采取预防措施甲,则预防措施费用为 万元,发生突发事件的概率为
万元,发生突发事件的概率为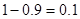 ,损失期望值为
,损失期望值为 (万元),
…………4分
(万元),
…………4分
所以总费用为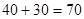 (万元)
.
…………5分
(万元)
.
…………5分
(3)若单独采用预防措施乙,则预防措施费用为 万元,发生突发事件的概率为
万元,发生突发事件的概率为 ,损失期望值为
,损失期望值为 (万元),
…………7分
(万元),
…………7分
所以总费用为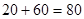 (万元)
.
…………8分
(万元)
.
…………8分
(4)若同时采用甲、乙两种预防措施,则预防措施费用为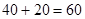 万元,发生突发事件的概率为
万元,发生突发事件的概率为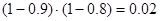 ,
…………10分
,
…………10分
损失期望值为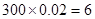 (万元),
…………11分
(万元),
…………11分
所以总费用为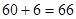 (万元).
…………12分
(万元).
…………12分
综合(1)(2)(3)(4),比较其总费用可知,同时采用甲、乙两种预防措施,总费用最少.
…………14分
【解析】略

(本题满分14分)某研究小组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试的成绩(百分制)如下表所示:
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
数学成绩 |
95 |
75 |
80 |
94 |
92 |
65 |
67 |
84 |
98 |
71 |
|
物理成绩 |
90 |
63 |
72 |
87 |
91 |
71 |
58 |
82 |
93 |
80 |
|
序号 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
数学成绩 |
67 |
93 |
64 |
78 |
77 |
90 |
57 |
84 |
72 |
83 |
|
物理成绩 |
77 |
82 |
48 |
85 |
69 |
91 |
61 |
82 |
78 |
86 |
若数学成绩90分(含90分)以上为优秀,物理成绩85分(含85分)以上为优秀。
⑴根据上表完成下面的 列联表:
列联表:
|
|
数学成绩优秀 |
数学成绩不优秀 |
合计 |
|
物理成绩优秀 |
|
|
|
|
物理成绩不优秀 |
|
12 |
|
|
合计 |
|
|
20 |
⑵根据⑴中表格的数据计算,有多少的把握,认为学生的数学成绩与物理成绩之间有关系?
(本题满分14分)
某校高三的某次数学测试中,对其中100名学生的成绩进行分析,按成绩分组,得到的频率分布表如下:
|
组号 |
分组 |
频数 |
频率 |
|
第1组 |
|
15 |
① |
|
第2组 |
|
② |
0.35 |
|
第3组 |
|
20 |
0.20 |
|
第4组 |
|
20 |
0.20 |
|
第5组 |
|
10 |
0.10 |
|
合计 |
|
100 |
1.00 |
(1)求出频率分布表中①、②位置相应的数据;
(2)为了选拔出最优秀的学生参加即将举行的数学竞赛,学校决定在成绩较高的第3、4、5组中分层抽样取5名学生,则第4、5组每组各抽取多少名学生?
(3)为了了解学生的学习情况,学校又在这5名学生当中随机抽取2名进行访谈,求第4组中至少有一名学生被抽到的概率是多少?
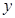 (万元)与年产量
(万元)与年产量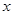 (吨)之间的函数关系式可以近似地表示为
(吨)之间的函数关系式可以近似地表示为 ,已知此生产线年产量最大为210吨.
,已知此生产线年产量最大为210吨. 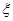 是一个随机变量,求随机变量
是一个随机变量,求随机变量 .
.