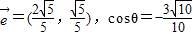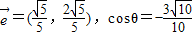题目内容
已知向量
是与单位向量
夹角为60°的任意向量,则对任意的正实数t,|t
-
|的最小值是( )
| a |
| b |
| a |
| b |
| A、0 | ||||
B、
| ||||
C、
| ||||
| D、1 |
分析:由题意利用两个向量的数量积的定义可得
•
=
,再根据|t
-
|=
=
,利用二次函数的性质求得它的最小值.
| a |
| b |
|
| ||
| 2 |
| a |
| b |
(t
|
(t|
|
解答:解:由题意可得
•
=|
|×1×cos60°=
,对任意的正实数t,
∵|t
-
|=
=
=
=
,
故当t|
|=
时,|t
-
|取得最小值为
=
,
故选:C.
| a |
| b |
| a |
|
| ||
| 2 |
∵|t
| a |
| b |
(t
|
(t
|
(t
|
(t|
|
故当t|
| a |
| 1 |
| 2 |
| a |
| b |
|
| ||
| 2 |
故选:C.
点评:本题主要考查两个向量的数量积的定义,求向量的模,二次函数的性质,属于中档题.

练习册系列答案
相关题目
已知两点A(4,1),B(7,-3),则与向量
同向的单位向量是( )
| AB |
A、±(
| ||||
B、(-
| ||||
C、(
| ||||
D、(
|
选择题:
(1)
在四边形ABCD中,若 ,则四边形ABCD是
,则四边形ABCD是
[
]|
A .矩形 |
B .菱形 |
|
C .正方形 |
D .平行四边形 |
(2)
已知向量 ,
,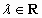 ,
,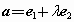 ,
,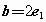 ,若向量a与b共线,则
,若向量a与b共线,则
[
]|
A . |
B . |
|
C . |
D . 或 或 |
(3)
已知a,b为两个单位向量,下列四个命题中正确的是[
]A
.a与b相等B
.如果a与b平行,那么a与b相等C
.a与b共线D
.如果a与b平行,那么a=b或a=-b(4)已知两个力 ,
, 的夹角为
的夹角为 ,它们的合力大小为10N,合力与
,它们的合力大小为10N,合力与 的夹角为
的夹角为 ,那么
,那么 的大小为
的大小为
[
]|
A . N N |
B .5N |
|
C .10N |
D . N N |
(5)
已知向量a表示“向东航行3km”,b表示“向南航行3km”,则a+b表示[
]|
A .向东南航行6km |
B .向东南航行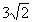 km km |
|
C .向东北航行 km km |
D .向东北航行6km |
(6)
河水的流速为2m/s,一艘小船想沿垂直于河岸方向以10m/s的速度驶向对岸,则小船的静水速度大小为[
]|
A .10m/s |
B . m/s m/s |
|
C . m/s m/s |
D .12m/s |
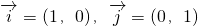 ,设与
,设与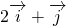 同向的单位向量为
同向的单位向量为 ,向量
,向量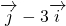 与向量
与向量 的夹角为θ,则下列说法正确的是
的夹角为θ,则下列说法正确的是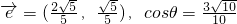
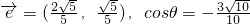
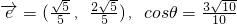
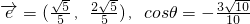
 ,设与
,设与 同向的单位向量为
同向的单位向量为 ,向量
,向量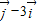 与向量
与向量 的夹角为θ,则下列说法正确的是( )
的夹角为θ,则下列说法正确的是( )