题目内容
(本小题满分12分)
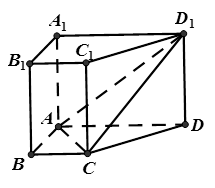
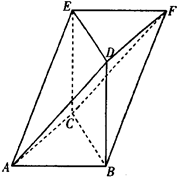
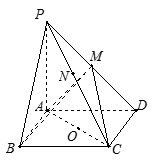
如图,在四棱柱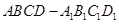 中,
中,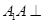 面
面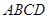 ,底面
,底面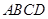 是直角梯形,
是直角梯形,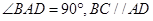 ,
,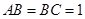 ,
,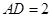 ,异面直线
,异面直线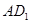 与
与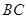 所成角为
所成角为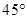 .
.
(1)求证: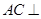 平面
平面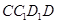 ;
;
(2)求直线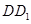 与平面
与平面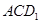 所成角的正弦值.
所成角的正弦值.
(1)根据线面垂直的判定定理,来得到垂直的证明。
(2) 
解析试题分析:解:(1)由已知得, 底面
底面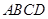 ,
,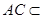 平面
平面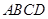 ,
,
所以 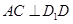 ……………2分
……………2分
又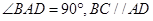 ,
,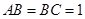 ,
,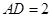 ,
,
所以 ,
,
所以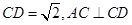 …………4分
…………4分
又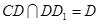 ,故
,故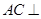 平面
平面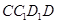 …………6分
…………6分
(2)因为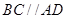 ,所以
,所以 为异面直线
为异面直线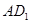 与
与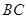 所成角,即为
所成角,即为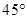 ,
,
又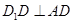 ,所以
,所以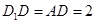 ……………8分
……………8分
过点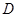 作
作 ,
, 为垂足,由(1)知,
为垂足,由(1)知, ,又
,又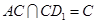 ,
,
所以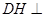 平面
平面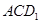 ,
,
故 是直线
是直线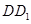 与平面
与平面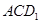 所成角,记为
所成角,记为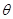 …………10分
…………10分
在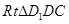 中,
中,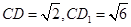 ,
,
所以 …………12分
…………12分
(2)另解:因为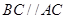 ,所以
,所以 为异面直线
为异面直线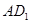 与
与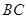 所成角,即为
所成角,即为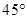 ,
,
又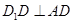 ,所以
,所以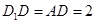 ……………8分
……………8分
设点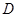 到平面
到平面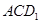 的距离为
的距离为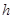 ,直线
,直线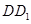 与平面
与平面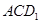 所成角为
所成角为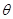 ,
,
又由(1)知,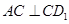 ,
, ,
,
由等体积法得: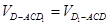 ,
,
即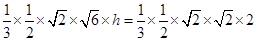 ,解得
,解得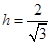 ………10分
………10分
所以 …………12分
…………12分
考点:本试题考查了空间几何体中线面角和面面垂直的知识。
点评:对于空间中点线面的位置关系,要熟练掌握基本的判定定理和性质定理,以及能结合向量的方法,合理的建立空间直角坐标系,结合空间向量的知识来表示角和距离的求解运用。属于中档题,这类试题的计算要细心,避免不不要的失分现象。

练习册系列答案
相关题目
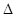 ABC的边AB,BC,CA上分别取D,E,F.使得DE=BE,FE=CE,又点O是△ADF的外心。
ABC的边AB,BC,CA上分别取D,E,F.使得DE=BE,FE=CE,又点O是△ADF的外心。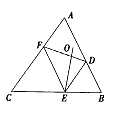
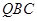 与直线
与直线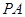 均垂直于
均垂直于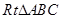 所在平面,且
所在平面,且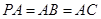 ,
,
 平面
平面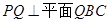 ,求
,求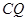 与平面
与平面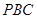 所成角的正弦值.
所成角的正弦值. 的最大面积及相应的x值.
的最大面积及相应的x值.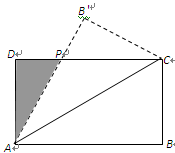
 ,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD
,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.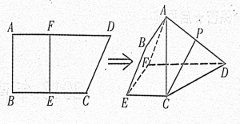
 底面
底面 为菱形,
为菱形, 平面
平面 ,
,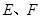 分别是
分别是 、
、 的中点.
的中点. 
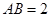 , 若
, 若 为线段
为线段 上的动点,
上的动点,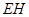 与平面
与平面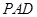 所成的最大角的正切值为
所成的最大角的正切值为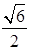 ,求此时异面直线AE和CH所成的角.
,求此时异面直线AE和CH所成的角.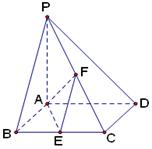
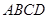 关于直线
关于直线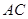 对称,
对称,
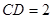 。
。 沿
沿 折起(如图二),使二面角
折起(如图二),使二面角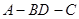 的余弦值等于
的余弦值等于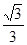 。对于图二,
。对于图二,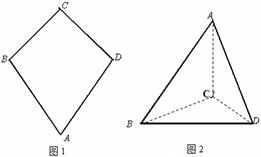
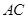 ;
;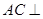 平面
平面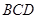 ;
; 所成角的正弦值。
所成角的正弦值。