题目内容
下列结论中正确命题的个数是
①命题p:“?x∈R,x2-2≥0”的否定形式为?p:“?x∈R,x2-2<0;
②若?p是q的必要条件,则p是?q的充分条件;
③“M>N”是“(
)M>(
)N”的充分不必要条件( )
①命题p:“?x∈R,x2-2≥0”的否定形式为?p:“?x∈R,x2-2<0;
②若?p是q的必要条件,则p是?q的充分条件;
③“M>N”是“(
| 2 |
| 3 |
| 2 |
| 3 |
| A、0 | B、1 | C、2 | D、3 |
分析:①根据命题“?x∈R,x2-2≥0”是特称命题,其否定为全称命题,即:“?x∈R,x2-2<0;②根据?p是q的必要条件,我们易得到q?-p的真假,然后根据逆否命题真假性相同,即可得到结论;③先判断“M>N”?“(
)M>(
)N”是否成立;再验证“(
)M>(
)N”?“M>N”是否成立,然后结合充要条件的定义即可得到答案.
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:①∵命题“?x∈R,x2-2≥0”是特称命题
∴否定命题为:“?x∈R,x2-2<0,故①正;.
②解:∵?p是q的必要条件,
∴q?-p为真命题,
故p?-q为真命题
故p是?q的充分条件,故②正确;
③∵函数y=(
)x在R上单调递减,
∴M>N?(
)M<(
)N,
因此“M>N”是“(
)M>(
)N”的既不充分也不必要条件,故③错,
故选C.
∴否定命题为:“?x∈R,x2-2<0,故①正;.
②解:∵?p是q的必要条件,
∴q?-p为真命题,
故p?-q为真命题
故p是?q的充分条件,故②正确;
③∵函数y=(
| 2 |
| 3 |
∴M>N?(
| 2 |
| 3 |
| 2 |
| 3 |
因此“M>N”是“(
| 2 |
| 3 |
| 2 |
| 3 |
故选C.
点评:此题考查特称命题和全称命题的否定以及判断充要条件的方法是:①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.属基础题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
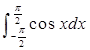 的值为2;
的值为2; ,则
,则 与
与 的夹角为钝角;
的夹角为钝角; ,则不等式
,则不等式 成立的概率是
成立的概率是 ;
; 的最小值为2.
的最小值为2. ”的否定形式为
”的否定形式为 “
“ ;
; 是q的必要条件,则p是
是q的必要条件,则p是 的充分条件;
的充分条件;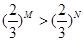 ”的充分不必要条件.
”的充分不必要条件.  ”的充分不必要条件( )
”的充分不必要条件( )