题目内容
下列结论中正确命题的序号为
①函数f(x)=x-sinx有三个零点;
②若
•
<0,则
与
的夹角为钝角;
③若a,b∈[0,1],则不等式a2+b2<
成立的概率是
;
④函数y=3x+3-x(x>0)的最小值为2.
③
③
.(写出所有正确命题的序号)①函数f(x)=x-sinx有三个零点;
②若
| a |
| b |
| a |
| b |
③若a,b∈[0,1],则不等式a2+b2<
| 1 |
| 4 |
| π |
| 16 |
④函数y=3x+3-x(x>0)的最小值为2.
分析:①利用导数判断函数的单调性,进而判断零点个数.②利用数量积的定义去判断夹角大小.③利用几何概型公式求概率.④使用基本不等式,当条件不成立时,则利用函数的单调性.
解答: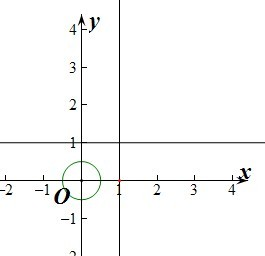 解:①函数的导数为f′(x)=1-cosx≥0恒成立,所以函数单调递增,使用f(x)=x-sinx最多有一个零点.所以①错误.
解:①函数的导数为f′(x)=1-cosx≥0恒成立,所以函数单调递增,使用f(x)=x-sinx最多有一个零点.所以①错误.
②当
与
共线且方向相反时,满足若
•
<0,但此时
与
的夹角为1800;所以②错误.
③若a,b∈[0,1],则不等式a2+b2<
成立的概率是P=
=
.如图.所以③正确.
④因为函数y=t+
在t>0时没有最小值,所以函数y=3x+3-x(x>0)没有最小值.所以④错误.
所以正确的只有③.
故答案为:③.
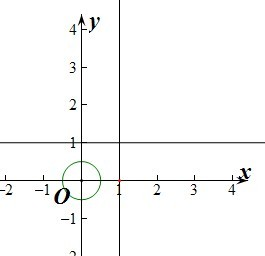 解:①函数的导数为f′(x)=1-cosx≥0恒成立,所以函数单调递增,使用f(x)=x-sinx最多有一个零点.所以①错误.
解:①函数的导数为f′(x)=1-cosx≥0恒成立,所以函数单调递增,使用f(x)=x-sinx最多有一个零点.所以①错误.②当
| a |
| b |
| a |
| b |
| a |
| b |
③若a,b∈[0,1],则不等式a2+b2<
| 1 |
| 4 |
| ||||
| 1×1 |
| π |
| 16 |
④因为函数y=t+
| 1 |
| t |
所以正确的只有③.
故答案为:③.
点评:本题考查各种命题的真假判断,正确利用相关知识进行推理,要求熟练进行应用.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
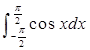 的值为2;
的值为2; ,则
,则 与
与 的夹角为钝角;
的夹角为钝角; ,则不等式
,则不等式 成立的概率是
成立的概率是 ;
; 的最小值为2.
的最小值为2. ”的否定形式为
”的否定形式为 “
“ ;
; 是q的必要条件,则p是
是q的必要条件,则p是 的充分条件;
的充分条件;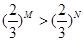 ”的充分不必要条件.
”的充分不必要条件.  ”的充分不必要条件( )
”的充分不必要条件( )