题目内容
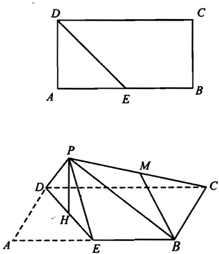 如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点.
如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点.
(1)求证:BM∥平面PDE;
(2)线段BC上是否存在一点N,使BC⊥平面PHN?试证明你的结论;
(3)求△PBC的面积.
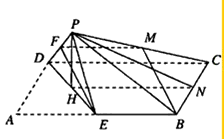 证明:(1)取PD的中点F,连接EF,FM
证明:(1)取PD的中点F,连接EF,FM由条件知:FM平行且等于DC的一半,EB平行且等于DC的一半
∴FM∥EB,且FM=EB
则四边形EFMB是平行四边形
则BM∥EF
∵BM?平面PDE,EF?平面PDE
∴BM∥平面PDE;
解:(2)当N为BC的中点时,BC⊥平面PHN,理由如下:
由题意得,HN为直角梯形BCDE的中位线
∴HN⊥BC
∵PB=PC
∴PN⊥BC
又∵HN∩PN=N
∴BC⊥平面PHN,
(3)由(2)中结论可得,BC⊥PH,
又∵PH⊥DE
故PH⊥底面BCDE
则PH⊥HN,即△PHN为直角三角形
∵AB=2AD=4,E为AB的中点
∴BC=2,HN=3,PH=
 ,则PN=
,则PN=
∴△PBC的面积S=
 •BC•PN=
•BC•PN=
分析:(1)取PD的中点F,连接EF,FM,由中位定理,及平行四边形判定定理易得四边形EFMB是平行四边形,进而BM∥EF,再由线面垂直的判定定理,即可得到BM∥平面PDE;
(2)取N为BC的中点,连接HN,易得HN为直角梯形BCDE的中位线,结合PB=PC,我们可得HN⊥BC,PN⊥BC,由线面垂直的判定定理可得BC⊥平面PHN;
(3)由已知中△PBC是以BC为底,PN为高的三角形,根据(2)的结论,我们易得△PHN为直角三角形,根据已知中AB=2AD=4,求出△PBC的底边长和高,代入三角形面积公式,即可得到答案.
点评:本题考查的知识点是直线与平面平行的判定,直线与平面垂直的判定,熟练掌握空间直线与平面位置关系的定义、判定定理、性质定理是解答本题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
 如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD.
如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD. 如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点.
如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点. 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=