题目内容
 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=| 1 | 2 |
(1)求证:CE⊥AB;
(2)在线段BC上找一点F,使DF∥平面ABE.
分析:(1)根据题意证出CE⊥BE,利用面面垂直的判定定理得出CE⊥平面ABE,结合AB?平面ABE,可得CE⊥AB;
(2)取线段BC的中点F,连结DF.根据ED、BF平行且相等,得四边形BEDF是平行四边形,从而DF∥BE,利用线面平行判定定理,即可证出DF∥平面ABE.
(2)取线段BC的中点F,连结DF.根据ED、BF平行且相等,得四边形BEDF是平行四边形,从而DF∥BE,利用线面平行判定定理,即可证出DF∥平面ABE.
解答:解:(1)∵矩形ABCD中,AB=
BC,E为AD的中点,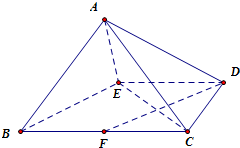
∴△ABE是等腰直角三角形,AE=AB,∠AEB=45°
同理可得DE=DC,∠DEC=45°,可得CE⊥BE
∵平面ABE⊥平面BCDE,平面ABE∩平面BCDE=BE
∴CE⊥平面ABE,
∵AB?平面ABE,∴CE⊥AB;
(2)取线段BC的中点F,连结DF
∵ED∥BF且ED=BF,∴四边形BEDF是平行四边形
可得DF∥BE
又∵DF?平面ABE,BE?平面ABE,
∴DF∥平面ABE,即在线段BC上存在中点F,满足DF∥平面ABE.
| 1 |
| 2 |

∴△ABE是等腰直角三角形,AE=AB,∠AEB=45°
同理可得DE=DC,∠DEC=45°,可得CE⊥BE
∵平面ABE⊥平面BCDE,平面ABE∩平面BCDE=BE
∴CE⊥平面ABE,
∵AB?平面ABE,∴CE⊥AB;
(2)取线段BC的中点F,连结DF
∵ED∥BF且ED=BF,∴四边形BEDF是平行四边形
可得DF∥BE
又∵DF?平面ABE,BE?平面ABE,
∴DF∥平面ABE,即在线段BC上存在中点F,满足DF∥平面ABE.
点评:本题给出平面图形的翻折,求证折出的几何体中线面平行与线线垂直.着重考查了空间平行、垂直位置关系的判定与证明等知识,属于中档题.

练习册系列答案
相关题目
 如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD.
如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD. 如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点.
如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点. 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: