题目内容
19.半径为R的球O中有一内接圆柱,当圆柱的侧面积最大时,则圆柱的表面积为( )| A. | 3πR2 | B. | 2πR2 | C. | $\frac{5π{R}^{2}}{2}$ | D. | $\frac{7π{R}^{2}}{2}$ |
分析 由题意圆柱的底面为球的截面,由球的截面性质可得出圆柱的高为h、底面半径为r与球的半径为R的关系,再用h和r表示出圆柱的侧面积,利用基本不等式求最值即可.
解答  解:如图为轴截面,令圆柱的高为h,底面半径为r,侧面积为S,
解:如图为轴截面,令圆柱的高为h,底面半径为r,侧面积为S,
则($\frac{h}{2}$)2+r2=R2,
即h=2 $\sqrt{{R}^{2}-{r}^{2}}$.
∵S=2πRh=4πr•$\sqrt{{R}^{2}-{r}^{2}}$=4π $\sqrt{{r}^{2}({R}^{2}-{r}^{2})}$≤4π $\sqrt{\frac{({r}^{2}+{R}^{2}-{r}^{2})^{2}}{4}}$=2πR2,
取等号时,内接圆柱底面半径为 $\frac{\sqrt{2}}{2}$R,高为 $\sqrt{2}$R.
圆柱的表面积为:2πR2+2π($\frac{\sqrt{2}}{2}$R)2=3πR2.
故选:A.
点评 本题考查球与圆柱的组合体问题、以及利用基本不等式求最值问题,难度一般.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
8.某单位为了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温:
由表中数据得线性方程$\widehat{y}$=$\widehat{a}$+$\widehat{b}$x中$\widehat{b}$=-2,据此预测当天气温为5℃时,用电量的度数约为( )
| 气温(℃) | 14 | 12 | 8 | 6 |
| 用电量(度) | 22 | 26 | 34 | 38 |
| A. | 60 | B. | 50 | C. | 40 | D. | 30 |

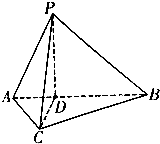 如图所示,三棱锥P-ABC中,点D为线段AB上一点,AC⊥BC,PD⊥平面ABC,AD=$\frac{1}{2}$DB,PD=BD,∠ABC=30°.
如图所示,三棱锥P-ABC中,点D为线段AB上一点,AC⊥BC,PD⊥平面ABC,AD=$\frac{1}{2}$DB,PD=BD,∠ABC=30°.