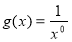题目内容
9.已知$\overrightarrow{a}$=(cosx,-2),$\overrightarrow{b}$=(sinx,1),$\overrightarrow{a}$∥$\overrightarrow{b}$,则tan(x-$\frac{π}{4}$)=-3.分析 由向量的平行关系可得tanx,代入两角差的正切公式计算可得.
解答 解:∵$\overrightarrow{a}$=(cosx,-2),$\overrightarrow{b}$=(sinx,1)且$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴1×cosx-(-2)×sinx=0,∴tanx=$\frac{sinx}{cosx}$=-$\frac{1}{2}$,
∴tan(x-$\frac{π}{4}$)=$\frac{tanx-tan\frac{π}{4}}{1+tanxtan\frac{π}{4}}$=$\frac{-\frac{1}{2}-1}{1+(-\frac{1}{2})×1}$=-3
故答案为:-3.
点评 本题考查两角和与差的正切函数,涉及平面向量的平行关系,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
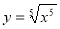 与
与
 与
与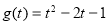 (
(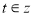 )
) 与
与
 与
与