题目内容
设正数数列{an}的前n项之和为Sn满足Sn=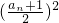
①先求出a1,a2,a3,a4的值,然后猜想数列{an}的通项公式,并用数学归纳法加以证明.
②设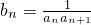 ,数列{bn}的前n项和为Tn.
,数列{bn}的前n项和为Tn.
解:①在 Sn=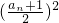 中,令n=1可得,a1=
中,令n=1可得,a1=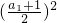 ,∴a1=1. 令n=2 可得,1+a2=
,∴a1=1. 令n=2 可得,1+a2=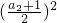 ,
,
a2 =3,同理可求,a3=5,a4=7.
猜测an=2n-1.
证明:当n=1时,猜测显然成立,假设 ak=2k-1,
则由 ak+1=sk+1-sk=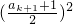 -
- =
=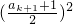 -k2,解得 ak+1=2k+1,
-k2,解得 ak+1=2k+1,
故n=k+1时,猜测仍然成立,
③∵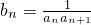 =
= =
= (
( -
- ),
),
∴Tn= [(1-
[(1- )+(
)+(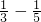 )+(
)+( 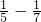 )+…+(
)+…+( -
- )]=
)]= (1-
(1- )
)
= .
.
分析:①求出数列的前若干项,归纳出一般结论,用数学归纳法证明.
③把通项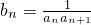 裂项变为
裂项变为  (
( -
- ),其前n项的和 Tn=
),其前n项的和 Tn=
 [(1-
[(1- )+(
)+(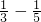 )+(
)+( 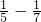 )+…+(
)+…+( -
- )]=
)]= (1-
(1- ) 化简可得结果.
) 化简可得结果.
点评:本题考查归纳推理,用数学归纳法证明等式,用裂项法进行数列求和,裂项求和是解题的难点.
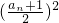 中,令n=1可得,a1=
中,令n=1可得,a1=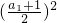 ,∴a1=1. 令n=2 可得,1+a2=
,∴a1=1. 令n=2 可得,1+a2=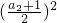 ,
,a2 =3,同理可求,a3=5,a4=7.
猜测an=2n-1.
证明:当n=1时,猜测显然成立,假设 ak=2k-1,
则由 ak+1=sk+1-sk=
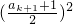 -
- =
=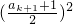 -k2,解得 ak+1=2k+1,
-k2,解得 ak+1=2k+1,故n=k+1时,猜测仍然成立,
③∵
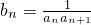 =
= =
= (
( -
- ),
),∴Tn=
 [(1-
[(1- )+(
)+(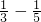 )+(
)+( 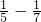 )+…+(
)+…+( -
- )]=
)]= (1-
(1- )
)=
 .
.分析:①求出数列的前若干项,归纳出一般结论,用数学归纳法证明.
③把通项
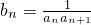 裂项变为
裂项变为  (
( -
- ),其前n项的和 Tn=
),其前n项的和 Tn= [(1-
[(1- )+(
)+(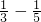 )+(
)+( 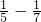 )+…+(
)+…+( -
- )]=
)]= (1-
(1- ) 化简可得结果.
) 化简可得结果.点评:本题考查归纳推理,用数学归纳法证明等式,用裂项法进行数列求和,裂项求和是解题的难点.

练习册系列答案
相关题目