题目内容
据统计某种汽车的最高车速为120千米∕时,在匀速行驶时每小时的耗油量y(升)与行驶速度y(千米∕时)之间有如下函数关系:y=
x3-
x+8.已知甲、乙两地相距100千米.
( I)若汽车以40千米∕时的速度匀速行驶,则从甲地到乙地需耗油多少升?
( II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
| 1 |
| 128000 |
| 3 |
| 80 |
( I)若汽车以40千米∕时的速度匀速行驶,则从甲地到乙地需耗油多少升?
( II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
分析:(Ⅰ)求出汽车从甲地到乙地行驶的时间,即可求得需耗油的升数;
(Ⅱ)当汽车的行驶速度为x千米∕时时,从甲地到乙地需行驶
小时,列出耗油函数关系式,利用导数可得最值.
(Ⅱ)当汽车的行驶速度为x千米∕时时,从甲地到乙地需行驶
| 100 |
| x |
解答:解:(Ⅰ)当x=40千米∕时时,汽车从甲地到乙地行驶了
=2.5(小时),
需耗油(
×403-
×40+8)×2.5=17.5(升).
所以,汽车以40千米∕时的速度匀速行驶,从甲地到乙地需耗油17.5升…(4分).
(Ⅱ)当汽车的行驶速度为x千米∕时时,从甲地到乙地需行驶
小时.设耗油量为h(x)升,
依题意,得h(x)=(
x3-
x+8)•
=
x2+
-
,其中,0<x≤120.…(7分)即h′(x)=
-
=
(0<x≤120).
令 h′(x)=0,得x=80
当x∈(0,80)时,h′(x)<0,函数单调递减;当x∈(80,120)时,h′(x)>0,函数单调递增
∴x=80时,从甲地到乙地耗油最少,最少为11.25升
∴所以当汽车以80千米∕时的速度行驶时,从甲地到乙地耗油最少,最少为11.25升.…(12分)
| 100 |
| 40 |
需耗油(
| 1 |
| 128000 |
| 3 |
| 80 |
所以,汽车以40千米∕时的速度匀速行驶,从甲地到乙地需耗油17.5升…(4分).
(Ⅱ)当汽车的行驶速度为x千米∕时时,从甲地到乙地需行驶
| 100 |
| x |
依题意,得h(x)=(
| 1 |
| 128000 |
| 3 |
| 80 |
| 100 |
| x |
| 1 |
| 1280 |
| 800 |
| x |
| 15 |
| 4 |
| x |
| 640 |
| 800 |
| x2 |
| x3-803 |
| 640x2 |
令 h′(x)=0,得x=80
当x∈(0,80)时,h′(x)<0,函数单调递减;当x∈(80,120)时,h′(x)>0,函数单调递增
∴x=80时,从甲地到乙地耗油最少,最少为11.25升
∴所以当汽车以80千米∕时的速度行驶时,从甲地到乙地耗油最少,最少为11.25升.…(12分)
点评:本题考查函数模型的构建,考查利用数学知识解决实际问题,考查导数知识的运用,属于中档题.

练习册系列答案
相关题目
 (升)与行驶速度
(升)与行驶速度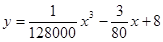 。已知甲、乙两地相距100千米。
。已知甲、乙两地相距100千米。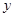 (升)与
(升)与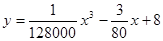 。已知甲、乙
。已知甲、乙