题目内容
已知:三次函数f(x)=x3+ax2+bx+c,在(-∞,-1),(2,+∞)上单调增,在(-1,2)上单调减,当且仅当x>4时,f(x)>x2-4x+5.
(1)求函数f (x)的解析式;
(2)若函数
 ,求h(x)的单调区间.
,求h(x)的单调区间.
【答案】分析:(1)由已知中三次函数f(x)=x3+ax2+bx+c,在(-∞,-1),(2,+∞)上单调增,在(-1,2)上单调减,可得f'(x)=3x2+2ax+b=0有两根-1,2,由韦达定理可以求出a,b的值,进而得到函数f (x)的解析式;
(2)由(1)中结论可得函数 的解析式,进而求出函数的导函数解析式,分类讨论后综合讨论结果可得答案.
的解析式,进而求出函数的导函数解析式,分类讨论后综合讨论结果可得答案.
解答:解:(1)∵f(x)在(-∞,-1),(2,+∞)上单增,(-1,2)上单减
∴f'(x)=3x2+2ax+b=0有两根-1,2
∴ …2
…2
令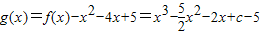 g′(x)=3x2-5x-2=(3x+1)(x-2)
g′(x)=3x2-5x-2=(3x+1)(x-2) 单调增,
单调增,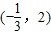 单调减
单调减
故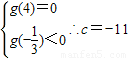
故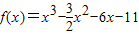 .…5
.…5
(2)∵f′(x)=3x2-3x-6
h(x)的定义域:…6∴h(x)=x+1-(m+1)ln(x+m)(x>-m且x≠2)…7
∴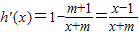 …9
…9
①m>-1时,-m<1.x∈(-m,1)2时,h'(x)<03;x∈(1,2)∪(2,+∞)4时,h'(x)>05
∴h(x)在(-m,1)单减;在(1,2),(2,+∞)上单增;
②-2<m≤-1时,h'(x)>0在定义域内恒成立,h(x)在(-m,2),(2,+∞)上单增
③当m≤-2时,此时h(x)的定义域为:(-m,+∞),h(x)在(-m,+∞)上单增
综上:当m≤-2时,h(x)在(-m,+∞)上单增;
当-2<m≤-1时,h(x)在(-m,2),(2,+∞)上单增;
当m>-1时,在(1,2),(2,+∞)上单增;在(-m,1)单减.…12
点评:本题考查的知识是函数的单调性与导数的关系,利用导数研究函数的单调性,其中(1)的关键是分析出f'(x)=3x2+2ax+b=0有两根-1,2,(2)的关键是对m值进行分类讨论.
(2)由(1)中结论可得函数
 的解析式,进而求出函数的导函数解析式,分类讨论后综合讨论结果可得答案.
的解析式,进而求出函数的导函数解析式,分类讨论后综合讨论结果可得答案.解答:解:(1)∵f(x)在(-∞,-1),(2,+∞)上单增,(-1,2)上单减
∴f'(x)=3x2+2ax+b=0有两根-1,2
∴
 …2
…2令
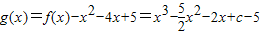 g′(x)=3x2-5x-2=(3x+1)(x-2)
g′(x)=3x2-5x-2=(3x+1)(x-2) 单调增,
单调增,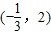 单调减
单调减故
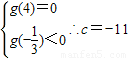
故
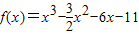 .…5
.…5(2)∵f′(x)=3x2-3x-6
h(x)的定义域:…6∴h(x)=x+1-(m+1)ln(x+m)(x>-m且x≠2)…7
∴
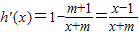 …9
…9①m>-1时,-m<1.x∈(-m,1)2时,h'(x)<03;x∈(1,2)∪(2,+∞)4时,h'(x)>05
∴h(x)在(-m,1)单减;在(1,2),(2,+∞)上单增;
②-2<m≤-1时,h'(x)>0在定义域内恒成立,h(x)在(-m,2),(2,+∞)上单增
③当m≤-2时,此时h(x)的定义域为:(-m,+∞),h(x)在(-m,+∞)上单增
综上:当m≤-2时,h(x)在(-m,+∞)上单增;
当-2<m≤-1时,h(x)在(-m,2),(2,+∞)上单增;
当m>-1时,在(1,2),(2,+∞)上单增;在(-m,1)单减.…12
点评:本题考查的知识是函数的单调性与导数的关系,利用导数研究函数的单调性,其中(1)的关键是分析出f'(x)=3x2+2ax+b=0有两根-1,2,(2)的关键是对m值进行分类讨论.

练习册系列答案
相关题目
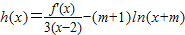 ,求h(x)的单调区间.
,求h(x)的单调区间.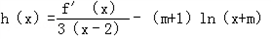 ,求h(x)的单调区间
,求h(x)的单调区间