题目内容
已知:三次函数f(x)=x3+ax2+bx+c,在(﹣∞,﹣1),(2,+∞)上单调增,在
(﹣1,2)上单调减,当且仅当x>4时,f(x)>x2﹣4x+5.
(1)求函数f (x)的解析式;
(2)若函数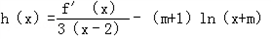 ,求h(x)的单调区间
,求h(x)的单调区间
(﹣1,2)上单调减,当且仅当x>4时,f(x)>x2﹣4x+5.
(1)求函数f (x)的解析式;
(2)若函数
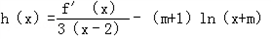 ,求h(x)的单调区间
,求h(x)的单调区间解:(1)∵f(x)在(﹣∞,﹣1),(2,+∞)上单增,(﹣1,2)上单减
∴f'(x)=3x2+2ax+b=0有两根﹣1,2
∴
令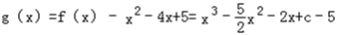
g′(x)=3x2﹣5x﹣2=(3x+1)(x﹣2)
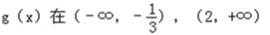 单调增,
单调增, 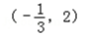 单调减
单调减
故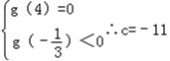 故
故 
(2)∵f′(x)=3x2﹣3x﹣6
h(x)的定义域:
∴h(x)=x+1﹣(m+1)ln(x+m)(x>﹣m且x≠2)
∴
①m>﹣1时,﹣m<1.x∈(﹣m,1)时,h'(x)<0;
x∈(1,2)∪(2,+∞)时,h'(x)>0
∴h(x)在(﹣m,1)单减;在(1,2),(2,+∞)上单增;
②﹣2<m≤﹣1时,h'(x)>0在定义域内恒成立,
h(x)在(﹣m,2),(2,+∞)上单增
③当m≤﹣2时,此时h(x)的定义域为:(﹣m,+∞),
h(x)在(﹣m,+∞)上单增
综上:当m≤﹣2时,h(x)在(﹣m,+∞)上单增;
当﹣2<m≤﹣1时,h(x)在(﹣m,2),(2,+∞)上单增;
当m>﹣1时,在(1,2),(2,+∞)上单增;在(﹣m,1)单减.
∴f'(x)=3x2+2ax+b=0有两根﹣1,2
∴

令
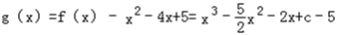
g′(x)=3x2﹣5x﹣2=(3x+1)(x﹣2)
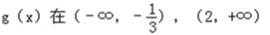 单调增,
单调增, 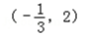 单调减
单调减故
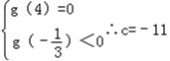 故
故 
(2)∵f′(x)=3x2﹣3x﹣6
h(x)的定义域:
∴h(x)=x+1﹣(m+1)ln(x+m)(x>﹣m且x≠2)
∴

①m>﹣1时,﹣m<1.x∈(﹣m,1)时,h'(x)<0;
x∈(1,2)∪(2,+∞)时,h'(x)>0
∴h(x)在(﹣m,1)单减;在(1,2),(2,+∞)上单增;
②﹣2<m≤﹣1时,h'(x)>0在定义域内恒成立,
h(x)在(﹣m,2),(2,+∞)上单增
③当m≤﹣2时,此时h(x)的定义域为:(﹣m,+∞),
h(x)在(﹣m,+∞)上单增
综上:当m≤﹣2时,h(x)在(﹣m,+∞)上单增;
当﹣2<m≤﹣1时,h(x)在(﹣m,2),(2,+∞)上单增;
当m>﹣1时,在(1,2),(2,+∞)上单增;在(﹣m,1)单减.

练习册系列答案
相关题目
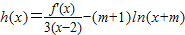 ,求h(x)的单调区间.
,求h(x)的单调区间. ,求h(x)的单调区间.
,求h(x)的单调区间.