题目内容
平面内动点M(x,y),
=(x-2,
y),
=(x+2,
y)且
•
=0
(Ⅰ)求点M的轨迹E的方程;
(Ⅱ)设直线:l:y=kx+m(k>0,m≠0)分别交x、y轴于点A、B,交曲线E于点C、D,且
=
①求k的值;
②若点N(
,1),求△NCD面积取得最大时直线l的方程.
| a |
| 2 |
| b |
| 2 |
| a |
| b |
(Ⅰ)求点M的轨迹E的方程;
(Ⅱ)设直线:l:y=kx+m(k>0,m≠0)分别交x、y轴于点A、B,交曲线E于点C、D,且
| CA |
| BD |
①求k的值;
②若点N(
| 2 |
(Ⅰ)设动点M(x,y).
∵
•
=0,∴(x-2)(x+2)+(
y)2=0,
化为
+
=1,即为点M的轨迹E的方程.
(Ⅱ)①在l:y=kx+m中分别令x=0,y=0可得B(0,m),A(-
,0).
设C(x1,y1),D(x2,y2),
由
得到(1+2k2)x2+4mkx+2m2-4=0,
△=16m2k2-4(1+2k2)(2m2-4)=32k2-8m2+16,
x1+x2=-
,x1x2=
.
∵
=
,∴-
-x1=x2,∴-
=-
,
又m≠0,化为4k2=1+2k2,k2=
,
∵k>0,∴k=
.
②|CD|=
|x1-x2|=
=
=
.
点N到CD的距离d=
=
|m|.
∴S△NCD=
|CD|•d=
•
•
|m|=
|m|=
≤
(
)=
.
当且仅当4-m2=m2时等号成立,即m2=2,解得m=±
.,此时△>0,
所以直线的方程为l:y=
x±
.
∵
| a |
| b |
| 2 |
化为
| x2 |
| 4 |
| y2 |
| 2 |
(Ⅱ)①在l:y=kx+m中分别令x=0,y=0可得B(0,m),A(-
| m |
| k |
设C(x1,y1),D(x2,y2),
由
|
△=16m2k2-4(1+2k2)(2m2-4)=32k2-8m2+16,
x1+x2=-
| 4mk |
| 1+2k2 |
| 2m2-4 |
| 1+2k2 |
∵
| CA |
| BD |
| m |
| k |
| 4mk |
| 1+2k2 |
| m |
| k |
又m≠0,化为4k2=1+2k2,k2=
| 1 |
| 2 |
∵k>0,∴k=
| ||
| 2 |
②|CD|=
| 1+k2 |
1+
|
| (x1+x2)2-4x1x2 |
|
| 2m2-4(m2-2) |
| 3(4-m2) |
点N到CD的距离d=
|
| ||
|
| ||
| 3 |
∴S△NCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3(4-m2) |
| ||
| 3 |
| ||
| 2 |
| 4-m2 |
| ||
| 2 |
| (4-m2)m2 |
| ||
| 2 |
| 4-m2+m2 |
| 2 |
| 2 |
当且仅当4-m2=m2时等号成立,即m2=2,解得m=±
| 2 |
所以直线的方程为l:y=
| ||
| 2 |
| 2 |

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
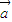 =(x-2,
=(x-2,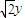 ),
),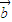 =(x+2,
=(x+2,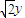 )且
)且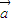 •
•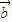 =0
=0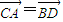
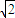 ,1),求△NCD面积取得最大时直线l的方程.
,1),求△NCD面积取得最大时直线l的方程. ,设动点P的轨迹为M,轨迹M与x轴的负半轴交于点A,过点F的直线交轨迹M于B、C两点.
,设动点P的轨迹为M,轨迹M与x轴的负半轴交于点A,过点F的直线交轨迹M于B、C两点.