题目内容
函数y=logax的定义域为[2，π]，若它的最大值比最小值大1，则底数a的值是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
分析：分类讨论，利用函数的单调性求出函数的最值，据最大值比最小值大1，求出底数a的值．
解答：解：当a＞1时，函数y=logax是定义域[2，π]内的增函数，logaπ-loga2=1，a=
，
当π＞a＞0时，函数y=logax是定义域[2，π]内的减函数，loga2-logaπ=1，a=
，
故选C．
| π |
| 2 |
当π＞a＞0时，函数y=logax是定义域[2，π]内的减函数，loga2-logaπ=1，a=
| 2 |
| π |
故选C．
点评：本题考查对数函数的单调性，以及利用对数函数的单调性求对数函数的最值．
练习册系列答案
名校课堂系列答案
相关题目
设a＞0，a≠1，函数y=logax的反函数和y=log
x的反函数的图象关于（ ）
| 1 |
| a |
| A、x轴对称 | B、y轴对称 |
| C、y=x轴对称 | D、原点对称 |
若函数y=f（x）是函数y=logax的反函数，且f(
)=2，则loga8等于（ ）
| 1 |
| 3 |
| A、3 | ||
| B、2 | ||
C、
| ||
| D、1 |
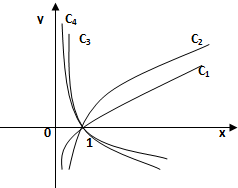如图是函数y=logax的图象，已知a值取