题目内容
已知二项式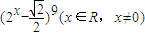 的展开式的第7项为
的展开式的第7项为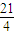 ,则
,则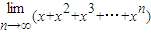 的值为 .
的值为 .
【答案】分析:通过展开式的第7项为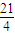 ,求出x的值,利用等比数列求出x+x2+x3+…+xn的和,然后求出极限即可.
,求出x的值,利用等比数列求出x+x2+x3+…+xn的和,然后求出极限即可.
解答:解:因为二项式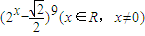 的展开式的第7项为
的展开式的第7项为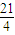 ,
,
所以 ,即
,即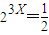 ,x=-
,x=- ,
,
x+x2+x3+…+xn=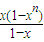 =
=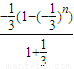 =
=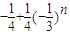 ,
,
∴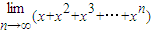 =
= =-
=- +
+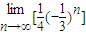 =
=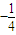 .
.
故答案为: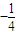 .
.
点评:本题是中档题,考查二项式定理系数的性质,数列的极限的求法,考查计算能力.
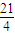 ,求出x的值,利用等比数列求出x+x2+x3+…+xn的和,然后求出极限即可.
,求出x的值,利用等比数列求出x+x2+x3+…+xn的和,然后求出极限即可.解答:解:因为二项式
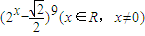 的展开式的第7项为
的展开式的第7项为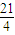 ,
,所以
 ,即
,即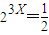 ,x=-
,x=- ,
,x+x2+x3+…+xn=
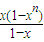 =
=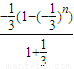 =
=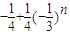 ,
,∴
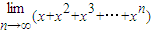 =
= =-
=- +
+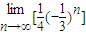 =
=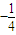 .
.故答案为:
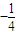 .
.点评:本题是中档题,考查二项式定理系数的性质,数列的极限的求法,考查计算能力.

练习册系列答案
相关题目
 的展开式的所有项的系数的和为
的展开式的所有项的系数的和为 ,展开式的所有二项式
,展开式的所有二项式 ,若
,若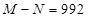 ,则
,则
 的展开式的所有项的系数的和为
的展开式的所有项的系数的和为 ,展开式的所有二项式的系数和为
,展开式的所有二项式的系数和为 ,若
,若 ,则
,则 .
. 的展开式的所有项的系数的和为
的展开式的所有项的系数的和为 ,展开式的所有二项式的系数和为
,展开式的所有二项式的系数和为 ,若
,若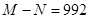 ,则
,则 .
.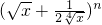 的展开式中,前三项的系数成等差数列.
的展开式中,前三项的系数成等差数列. 的展开式的二项式系数之和为32,则展开式中含x项的系数是( )
的展开式的二项式系数之和为32,则展开式中含x项的系数是( )