题目内容
平面直角坐标系下,点P((x,y)满足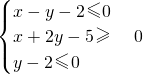 ,线段AB是圆x2+(y+2)2=1的任意一条直径,则PA•PB的最小值为________.
,线段AB是圆x2+(y+2)2=1的任意一条直径,则PA•PB的最小值为________.
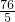
分析:先画出满足条件
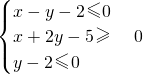 的平面区域,再把
的平面区域,再把 •
• 的最小值转化为圆心到可行域内的点的距离的最小值即可.
的最小值转化为圆心到可行域内的点的距离的最小值即可.解答:
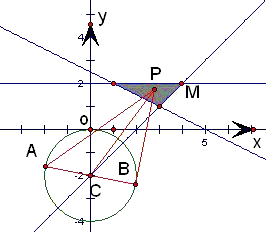 解:设P(x,y),线段 AB是 x2+(y+2)2=1的任意直径,
解:设P(x,y),线段 AB是 x2+(y+2)2=1的任意直径,C(0,-2)为圆心,如图,
 •
• =(
=( +
+ )•(
)•( +
+ )
)=(
 +
+ )•(
)•( -
- )
)=(
 )2-(
)2-( )2
)2=|
 |2-1,
|2-1,P满足
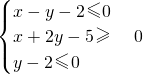 ,
,结合图形,只须求出圆心C到直线x+2y-5=0的距离d即为|
 |
|的最小值,
d=
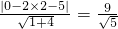
所以
 •
• 的最小值=(
的最小值=(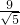 )2-1=
)2-1=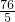 .
.故答案为:
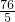 .
.点评:本题属于线性规划中的延伸题,对于可行域不要求线性目标函数的最值,而是求可行域内的点与C之间的距离问题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
 (2012•天门模拟)(1)如图,圆O的直径AB=8,C为圆周上一点,BC=4,过点C作圆的切线l,过点A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段AE的长为
(2012•天门模拟)(1)如图,圆O的直径AB=8,C为圆周上一点,BC=4,过点C作圆的切线l,过点A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段AE的长为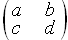 的形式,称为二行二列矩阵,定义矩阵的一种运算
的形式,称为二行二列矩阵,定义矩阵的一种运算 ,设运算的几何意义为平面直角坐标系下的点(x,y)在矩阵
,设运算的几何意义为平面直角坐标系下的点(x,y)在矩阵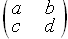 的作用下变换为点(ax+by,cx+dy),给出下列命题:
的作用下变换为点(ax+by,cx+dy),给出下列命题:
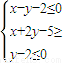 ,线段AB是圆x2+(y+2)2=1的任意一条直径,则PA•PB的最小值为 .
,线段AB是圆x2+(y+2)2=1的任意一条直径,则PA•PB的最小值为 .