��Ŀ����
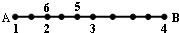 ��2012•������һģ����֪�߶�AB����10��ȷ���ĵ㣨�����˵�A��B�����ֶ���Щ�������������
��2012•������һģ����֪�߶�AB����10��ȷ���ĵ㣨�����˵�A��B�����ֶ���Щ�����������������A��B��A��B�������б���������ͬ����㲻����ʱ�͡���ͷ������������
��ͼ���ڵ�A�ϱ�1����Ϊ��1��Ȼ��ӵ�1��ʼ�����ڶ�����������2����Ϊ��2���ٴӵ�2��ʼ������������������3����Ϊ��3��������n�ĵ��Ϊ��n������������һֱ������ȥ��ֱ��1��2��3������2012������ǵ����ϣ����2012�ϵ����б�ǵ����У���С����
3
3
��������ȷ������2012����1+2+3+��+2012=2025078�ţ�2025078����18������Ϊ6�����߶εĵ�6�����Ϊ2012����ô6+18n=1+2+3+��+k=
����12+36n=k��k+1������n=0�����ɵý��ۣ�
| k(k+1) |
| 2 |
����⣺�DZ���1Ϊ��1�ţ����ڶ���Щ�����������������A��B��A��B�������б���������ͬ����㲻����ʱ�͡���ͷ�����������������2����1+2�ţ�����3����1+2+3�ţ�����4����1+2+3+4����������2012����1+2+3+��+2012=2025078�ţ�����ΪһԲ�ܣ���Բ���Ϲ�18����
����2025078����18������Ϊ6�����߶εĵ�6�����Ϊ2012����ô6+18n=1+2+3+��+k=
��
��12+36n=k��k+1����
��n=0ʱ��k��k+1��=12��k=3�������⣬����n������kҲ����
���ԣ�����2012���Ǹ����ϱ������С��Ϊ3��
�ʴ�Ϊ��3
����2025078����18������Ϊ6�����߶εĵ�6�����Ϊ2012����ô6+18n=1+2+3+��+k=
| k(k+1) |
| 2 |
��12+36n=k��k+1����
��n=0ʱ��k��k+1��=12��k=3�������⣬����n������kҲ����
���ԣ�����2012���Ǹ����ϱ������С��Ϊ3��
�ʴ�Ϊ��3
���������⿼���������������ѧ�������������������������е��⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��2012•������һģ����һԲ���ϸ���1000���㣮����ͼ��ȡ����һ��������1������㿪ʼ��˳ʱ�뷽�������ڶ�����������2���ӱ����2�ĵ㿪ʼ��˳ʱ�뷽��������������������3�������������ֱ��1��2��3������2012������ǵ����ϣ�Բ������Щ������Щ���ܻ����ϲ�ֹһ�������ڱ����2012����һ���ϵ����б�ǵ�������С����
��2012•������һģ����һԲ���ϸ���1000���㣮����ͼ��ȡ����һ��������1������㿪ʼ��˳ʱ�뷽�������ڶ�����������2���ӱ����2�ĵ㿪ʼ��˳ʱ�뷽��������������������3�������������ֱ��1��2��3������2012������ǵ����ϣ�Բ������Щ������Щ���ܻ����ϲ�ֹһ�������ڱ����2012����һ���ϵ����б�ǵ�������С���� ��2012•������һģ�����߳��ֱ�Ϊ1��2��3������n��n+1������n��N*���������ε�����һ���γ���ͼ��ʾ��ͼ�Σ���С�������μǸ���Ӱ�������ڵ�ͼ��Ϊ��1������2����������n����Ӱ����ͼ�Σ�����֪����1����Ӱ����ͼ�ε��ܳ�Ϊ8����ǰn����Ӱ����ͼ�ε��ܳ���ƽ��ֵΪf��n����������{an}����
��2012•������һģ�����߳��ֱ�Ϊ1��2��3������n��n+1������n��N*���������ε�����һ���γ���ͼ��ʾ��ͼ�Σ���С�������μǸ���Ӱ�������ڵ�ͼ��Ϊ��1������2����������n����Ӱ����ͼ�Σ�����֪����1����Ӱ����ͼ�ε��ܳ�Ϊ8����ǰn����Ӱ����ͼ�ε��ܳ���ƽ��ֵΪf��n����������{an}����