题目内容
设t>0,已知函数f (x)=x2(x-t)的图象与x轴交于A、B两点.(1)求函数f (x)的单调区间;
(2)设函数y=f(x)在点P(x,y)处的切线的斜率为k,当x∈(0,1]时,k≥-
 恒成立,求t的最大值;
恒成立,求t的最大值;(3)有一条平行于x轴的直线l恰好与函数y=f(x)的图象有两个不同的交点C,D,若四边形ABCD为菱形,求t的值.
【答案】分析:(1)由导数大于0可求单调递增区间,导数小于0可求单调递减区间;
(2)当x∈(0,1]时,k≥- 恒成立,转化为即t≤
恒成立,转化为即t≤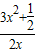 ,x∈(0,1]只需求其最小值;
,x∈(0,1]只需求其最小值;
(3)由题意画出图象,用距离相等可求t的值.
解答:解:(1)∵函数f (x)=x2(x-t)=x3-tx2,∴f′(x)=3x2-2tx=x(3x-2t)
令x(3x-2t)<0,解得0<x< ,(t>0);令x(3x-2t)>0,解得x<0,或x>
,(t>0);令x(3x-2t)>0,解得x<0,或x>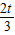 ,
,
故函数f (x)的单调递减区间为(0, );单调递增区间为(-∞,0)和(
);单调递增区间为(-∞,0)和( ,+∞).
,+∞).
(2)由题意及(1)知,k=f′(x)=3x2-2tx,x∈(0,1],k≥- 恒成立
恒成立
即当x∈(0,1]时,3x2-2tx≥- 恒成立,即t≤
恒成立,即t≤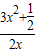 ,x∈(0,1]
,x∈(0,1]
即函数g(x)= ,x∈(0,1]只需求出其最小值即可,
,x∈(0,1]只需求出其最小值即可,
g(x)=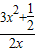 =
= ≥2
≥2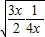 =
= ,当且仅当
,当且仅当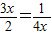 ,
,
即x= ∈(0,1]时,取到等号,故
∈(0,1]时,取到等号,故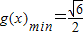 可得t≤
可得t≤
故t的最大值为: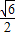
(3)由以上可知f(x)的图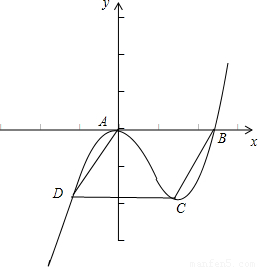 由f(
由f( )=-
)=-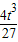 即C(
即C(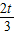 ,
,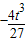 )B(t,0)
)B(t,0)
由于四边形ABCD为菱形,故|AB|=|BC|即t= 解得t=
解得t=
故t的值为: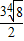
点评:本题为导数的综合应用,设计单调区间的求解,恒成立问题以及由性质画图象,属中档题.
(2)当x∈(0,1]时,k≥-
 恒成立,转化为即t≤
恒成立,转化为即t≤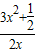 ,x∈(0,1]只需求其最小值;
,x∈(0,1]只需求其最小值;(3)由题意画出图象,用距离相等可求t的值.
解答:解:(1)∵函数f (x)=x2(x-t)=x3-tx2,∴f′(x)=3x2-2tx=x(3x-2t)
令x(3x-2t)<0,解得0<x<
 ,(t>0);令x(3x-2t)>0,解得x<0,或x>
,(t>0);令x(3x-2t)>0,解得x<0,或x>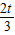 ,
,故函数f (x)的单调递减区间为(0,
 );单调递增区间为(-∞,0)和(
);单调递增区间为(-∞,0)和( ,+∞).
,+∞).(2)由题意及(1)知,k=f′(x)=3x2-2tx,x∈(0,1],k≥-
 恒成立
恒成立即当x∈(0,1]时,3x2-2tx≥-
 恒成立,即t≤
恒成立,即t≤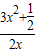 ,x∈(0,1]
,x∈(0,1]即函数g(x)=
 ,x∈(0,1]只需求出其最小值即可,
,x∈(0,1]只需求出其最小值即可,g(x)=
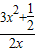 =
= ≥2
≥2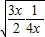 =
= ,当且仅当
,当且仅当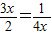 ,
,即x=
 ∈(0,1]时,取到等号,故
∈(0,1]时,取到等号,故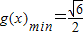 可得t≤
可得t≤
故t的最大值为:
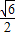
(3)由以上可知f(x)的图
 由f(
由f( )=-
)=-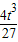 即C(
即C(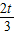 ,
,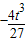 )B(t,0)
)B(t,0)由于四边形ABCD为菱形,故|AB|=|BC|即t=
 解得t=
解得t=
故t的值为:
点评:本题为导数的综合应用,设计单调区间的求解,恒成立问题以及由性质画图象,属中档题.

练习册系列答案
相关题目
 恒成立,求t的最大值;
恒成立,求t的最大值; 恒成立,求t的最大值;
恒成立,求t的最大值; 恒成立,求t的最大值;
恒成立,求t的最大值;