题目内容
一个正四面体的所有棱长都为
，四个顶点在同一球面上，求此球的表面积．
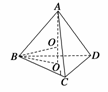[解析] 如图，设正四面体ABCD的高为AO1，设球的球心为O，半径为R，则O1B＝
BC＝
.
在Rt△AO1B中，
AO1＝
＝
＝
.
在Rt△OO1B中，O1O2＝R2－()2＝R2－
.
∴AO1＝R＋
＝，
∴R＝
，∴S球＝4πR2＝4π×()2＝3π.
故球的表面积为3π.
练习册系列答案
相关题目
题目内容
一个正四面体的所有棱长都为，四个顶点在同一球面上，求此球的表面积．
[解析] 如图，设正四面体ABCD的高为AO1，设球的球心为O，半径为R，则O1B＝BC＝.
在Rt△AO1B中，
AO1＝＝＝.
在Rt△OO1B中，O1O2＝R2－()2＝R2－.
∴AO1＝R＋＝，
∴R＝，∴S球＝4πR2＝4π×()2＝3π.
故球的表面积为3π.
D.6π
D.6π
D.6π