题目内容
已知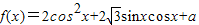 ,a为实常数.
,a为实常数.(I)求f(x)的最小正周期;
(II)若f(x)在
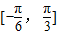 上最大值与最小值之和为3,求a的值.
上最大值与最小值之和为3,求a的值.
【答案】分析:(I)利用降幂公式(逆用二倍角余弦公式),结合辅助角公式,我们可将函数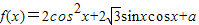 的解析式化为正弦型函数的形式,进而根据T=
的解析式化为正弦型函数的形式,进而根据T=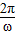 ,即可求出f(x)的最小正周期;
,即可求出f(x)的最小正周期;
(II)由(I)中函数的解析式,我们易分析出函数f(x)在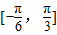 上的最大值和最小值(含参数a),进而根据f(x)在
上的最大值和最小值(含参数a),进而根据f(x)在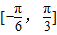 上最大值与最小值之和为3,构造出含a的方程,解方程即可求出a的值.
上最大值与最小值之和为3,构造出含a的方程,解方程即可求出a的值.
解答:解:(I)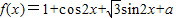 =
=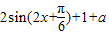
所以f(x)的最小正周期T=π; …(5分)
(II)∵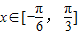 ,则
,则 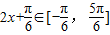 ∴
∴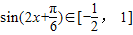
所以f(x)是最大值为3+a,最小值为a
依题意有:3+2a=3,∴a=0…(10分)
点评:本题考查的知识点是三角函数的化简求值,两角和与差的正弦函数,正弦函数的定义域和值域,其中利用降幂公式(逆用二倍角余弦公式),结合辅助角公式,化简函数的解析式是解答本题的关键.
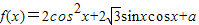 的解析式化为正弦型函数的形式,进而根据T=
的解析式化为正弦型函数的形式,进而根据T=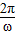 ,即可求出f(x)的最小正周期;
,即可求出f(x)的最小正周期;(II)由(I)中函数的解析式,我们易分析出函数f(x)在
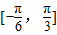 上的最大值和最小值(含参数a),进而根据f(x)在
上的最大值和最小值(含参数a),进而根据f(x)在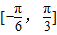 上最大值与最小值之和为3,构造出含a的方程,解方程即可求出a的值.
上最大值与最小值之和为3,构造出含a的方程,解方程即可求出a的值.解答:解:(I)
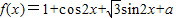 =
=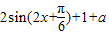
所以f(x)的最小正周期T=π; …(5分)
(II)∵
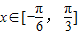 ,则
,则 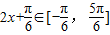 ∴
∴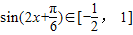
所以f(x)是最大值为3+a,最小值为a
依题意有:3+2a=3,∴a=0…(10分)
点评:本题考查的知识点是三角函数的化简求值,两角和与差的正弦函数,正弦函数的定义域和值域,其中利用降幂公式(逆用二倍角余弦公式),结合辅助角公式,化简函数的解析式是解答本题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
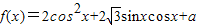 ,a为实常数.
,a为实常数.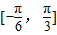 上最大值与最小值之和为3,求a的值.
上最大值与最小值之和为3,求a的值.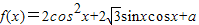 ,a为实常数.
,a为实常数. 上最大值与最小值之和为3,求a的值.
上最大值与最小值之和为3,求a的值.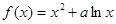 (a为实常数).
(a为实常数).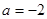 ,求证:函数
,求证:函数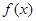 在(1,+.∞)上是增函数;
在(1,+.∞)上是增函数; 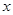 值;
值;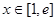 ,使得
,使得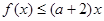 成立,求实数a的取值范围.
成立,求实数a的取值范围.