题目内容
如图在三角形ABC中,E为斜边AB的中点,CD⊥AB,AB=1,则 的最大值是 .
的最大值是 .
【答案】分析:设CA=x,CB=y,则x2+y2=1,求出CD,然后根据数量积公式求出 ,然后利用基本不等式进行求解,即可求出最大值.
,然后利用基本不等式进行求解,即可求出最大值.
解答:解:设CA=x,CB=y,则x2+y2=1
CD=
∴

∴ =
= x4•y2=
x4•y2= x4(1-x2)=2•
x4(1-x2)=2• •
• (1-x2)≤2
(1-x2)≤2 =
= .
.
故答案为:
点评:本题主要考查了向量的数量积,以及基本不等式求最值,有一定的难度,属于中档题.
 ,然后利用基本不等式进行求解,即可求出最大值.
,然后利用基本不等式进行求解,即可求出最大值.解答:解:设CA=x,CB=y,则x2+y2=1
CD=

∴


∴
 =
= x4•y2=
x4•y2= x4(1-x2)=2•
x4(1-x2)=2• •
• (1-x2)≤2
(1-x2)≤2 =
= .
.故答案为:

点评:本题主要考查了向量的数量积,以及基本不等式求最值,有一定的难度,属于中档题.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目
 如图在三角形ABC中,E为斜边AB的中点,CD⊥AB,AB=1,则
如图在三角形ABC中,E为斜边AB的中点,CD⊥AB,AB=1,则 的最大值是 .
的最大值是 .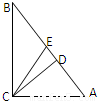
 的最大值是 .
的最大值是 .
 的最大值是 .
的最大值是 .