题目内容
(Ⅰ)求值:sin690°•sin150°+cos930°•cos(-870°)+tan120°•tan1050°;
(Ⅱ)已知角α的终边上有一点P(1,2),求
的值.
(Ⅱ)已知角α的终边上有一点P(1,2),求
| 4sinα-2cosα | 5sinα+3cosα |
分析:(Ⅰ)利用诱导公式把要求的式子化为-tan30°sin30°+cos150°cos150°+tan60°tan30°,再利用特殊角的三角函数值求得结果.
(Ⅱ)根据已知角α的终边上有一点P(1,2),可得tanα=2,再根据
=
,运算求得结果.
(Ⅱ)根据已知角α的终边上有一点P(1,2),可得tanα=2,再根据
| 4sinα-2cosα |
| 5sinα+3cosα |
| 4tanα-2 |
| 5tanα+3 |
解答:解:(Ⅰ)sin690°•sin150°+cos930°•cos(-870°)+tan120°•tan1050°
=sin(720°-30°)sin30°+cos(3×360°-150°)cos(720°+150°)+(-tan60°)tan(3×360°-30°)
=-tan30°sin30°+cos150°cos150°+tan60°tan30°=-
×
+
+1=
.
(Ⅱ)∵已知角α的终边上有一点P(1,2),∴tanα=2,故
=
=
=
.
=sin(720°-30°)sin30°+cos(3×360°-150°)cos(720°+150°)+(-tan60°)tan(3×360°-30°)
=-tan30°sin30°+cos150°cos150°+tan60°tan30°=-
| ||
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
(Ⅱ)∵已知角α的终边上有一点P(1,2),∴tanα=2,故
| 4sinα-2cosα |
| 5sinα+3cosα |
| 4tanα-2 |
| 5tanα+3 |
| 8-2 |
| 10+3 |
| 6 |
| 13 |
点评:本题主要考查同角三角函数的基本关系的应用,诱导公式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.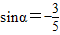 ,且α为第三象限角,求cosα,cos2α的值
,且α为第三象限角,求cosα,cos2α的值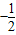 .
.