题目内容
设实数x,y满足x2+(y-1)2=1,若对满足条件x,y,不等式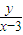 +c≥0恒成立,则c的取值范围是 .
+c≥0恒成立,则c的取值范围是 .
【答案】分析:由题意,借助已知动点在圆x2+(y-1)2=1上任意动,而所求式子  的形式可以联想成在单位圆上动点P与点(3,0)构成的直线的斜率,进而不等式
的形式可以联想成在单位圆上动点P与点(3,0)构成的直线的斜率,进而不等式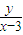 ≥-c恒成立,即-c小于等于
≥-c恒成立,即-c小于等于 的最小值,从而得出c的取值范围.
的最小值,从而得出c的取值范围.
解答: 解:由题意作出如下图形:
解:由题意作出如下图形:
令k=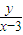 ,则k可看作圆x2+(y-1)2=1上的动点P到点(3,0)的连线的斜率,由于连线与圆相切时,斜率k最小,最小值为-
,则k可看作圆x2+(y-1)2=1上的动点P到点(3,0)的连线的斜率,由于连线与圆相切时,斜率k最小,最小值为- ,
,
∵不等式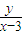 +c≥0恒成立,
+c≥0恒成立,
∴不等式 ≥-c恒成立,即-c小于等于
≥-c恒成立,即-c小于等于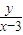 的最小值,
的最小值,
即:-c≤- ⇒c≥
⇒c≥
则c的取值范围是c≥ .
.
故答案为:c≥
点评:此题重点考查了已知两点坐标写斜率,及直线与圆的相切与相交的关系,还考查了利用几何思想解决代数式子的等价转化的思想.
 的形式可以联想成在单位圆上动点P与点(3,0)构成的直线的斜率,进而不等式
的形式可以联想成在单位圆上动点P与点(3,0)构成的直线的斜率,进而不等式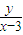 ≥-c恒成立,即-c小于等于
≥-c恒成立,即-c小于等于 的最小值,从而得出c的取值范围.
的最小值,从而得出c的取值范围.解答:
 解:由题意作出如下图形:
解:由题意作出如下图形:令k=
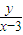 ,则k可看作圆x2+(y-1)2=1上的动点P到点(3,0)的连线的斜率,由于连线与圆相切时,斜率k最小,最小值为-
,则k可看作圆x2+(y-1)2=1上的动点P到点(3,0)的连线的斜率,由于连线与圆相切时,斜率k最小,最小值为- ,
,∵不等式
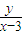 +c≥0恒成立,
+c≥0恒成立,∴不等式
 ≥-c恒成立,即-c小于等于
≥-c恒成立,即-c小于等于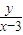 的最小值,
的最小值,即:-c≤-
 ⇒c≥
⇒c≥
则c的取值范围是c≥
 .
.故答案为:c≥

点评:此题重点考查了已知两点坐标写斜率,及直线与圆的相切与相交的关系,还考查了利用几何思想解决代数式子的等价转化的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目