题目内容
设实数x,y满足x2+(y-1)2=1,若不等式x+y+C≥0对任意的x,y都成立,则实数C的取值范围是( )
分析:画出曲线与直线的图象,结合图象求出临界点的c的值,然后确定c的范围.
解答:解: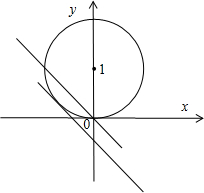
由题意画出曲线的图形,满足题意实数C的取值范围,就是图象中切线的上方,
当且仅当,圆心到直线的距离等于半径时,即1=
,解得c=±
-1,由图象可知
c=
-1.
所以满足题意的c为:c≥
-1.
故选D.

由题意画出曲线的图形,满足题意实数C的取值范围,就是图象中切线的上方,
当且仅当,圆心到直线的距离等于半径时,即1=
| |0+1+c| | ||
|
| 2 |
c=
| 2 |
所以满足题意的c为:c≥
| 2 |
故选D.
点评:本题是中档题,考查简单线性规划的应用,注意判断临界点的值,是解题的关键.

练习册系列答案
相关题目