题目内容
已知顶点在坐标原点,焦点在x轴正半轴的抛物线上有一点A(
,m),A点到抛物线焦点的距离为1.
(1)求该抛物线的方程;
(2)设M(x0,y0)为抛物线上的一个定点,过M作抛物线的两条互相垂直的弦MP,MQ,求证:PQ恒过定点(x0+2,-y0).
(3)直线x+my+1=0与抛物线交于E,F两点,在抛物线上是否存在点N,使得△NEF为以EF为斜边的直角三角形.
| 1 |
| 2 |
(1)求该抛物线的方程;
(2)设M(x0,y0)为抛物线上的一个定点,过M作抛物线的两条互相垂直的弦MP,MQ,求证:PQ恒过定点(x0+2,-y0).
(3)直线x+my+1=0与抛物线交于E,F两点,在抛物线上是否存在点N,使得△NEF为以EF为斜边的直角三角形.
(1)由题意可设抛物线的方程为y2=2px,则由抛物线的定义可得
+
=1,即p=1,
所以抛物线的方程为 y2=2x.
(2)由题意知直线PQ与x轴不平行,设PQ所在直线方程为x=my+n,代入y2=2x中得 y2-2my-2n=0.
所以y1+y2=2m,y1y=-2n,其中y1,y2分别是P,Q的纵坐标,
因为MP⊥MQ,所以kMP•kMQ=-1.
即
•
=-1,所以(y1+y0)(y2+y0)=-4.
y1•y2+(y1+y2)y0+y02+4=0,(-2n)+2my0+2x0+4=0,即n=my0+x0+2.
所以直线PQ的方程为x=my+my0+x0+2,
即x=m(y+y0)+x0+2,它一定过定点(x0+2,-y0).
(3)假设N(x0,y0)为满足条件的点,则由(2)知,点(x0+2,-y0)在直线x+my+1=0上,
所以x0+2-my0+1=0,(x0,y0)是方程组
的解,
消去x得y2-2my+6=0,△=4m2-24≥0所以存在点N满足条件.
| p |
| 2 |
| 1 |
| 2 |
所以抛物线的方程为 y2=2x.
(2)由题意知直线PQ与x轴不平行,设PQ所在直线方程为x=my+n,代入y2=2x中得 y2-2my-2n=0.
所以y1+y2=2m,y1y=-2n,其中y1,y2分别是P,Q的纵坐标,
因为MP⊥MQ,所以kMP•kMQ=-1.
即
| y1-y0 |
| x1-x0 |
| y2-y0 |
| x2-x0 |
y1•y2+(y1+y2)y0+y02+4=0,(-2n)+2my0+2x0+4=0,即n=my0+x0+2.
所以直线PQ的方程为x=my+my0+x0+2,
即x=m(y+y0)+x0+2,它一定过定点(x0+2,-y0).
(3)假设N(x0,y0)为满足条件的点,则由(2)知,点(x0+2,-y0)在直线x+my+1=0上,
所以x0+2-my0+1=0,(x0,y0)是方程组
|
消去x得y2-2my+6=0,△=4m2-24≥0所以存在点N满足条件.

练习册系列答案
相关题目
 轴正半轴的抛物线上有一点
轴正半轴的抛物线上有一点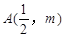 ,
, 点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设
点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设 为抛物线上的一个定点,过
为抛物线上的一个定点,过 作抛物线的两条互相垂直的弦
作抛物线的两条互相垂直的弦 ,
, ,求证:
,求证: 恒过定点
恒过定点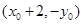 .(3)直线
.(3)直线 与抛物线交于
与抛物线交于 ,
, 两点,在抛物线上是否存在点
两点,在抛物线上是否存在点 ,使得△
,使得△ 为以
为以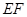 为斜边的直角三角形.
为斜边的直角三角形.