题目内容

17．已知变量x、y满足：$\left\{\begin{array}{l}{x≥0}\\{x+3≥2y}\\{y≥2x}\end{array}\right.$，则z=（$\sqrt{2}$）x+y的最大值为2$\sqrt{2}$．

分析 首先画出可行域，求出x+y的最大值，然后求z 的最大值．

解答 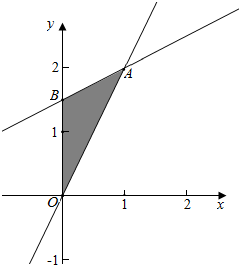解：不等式组表示的平面区域如图当直线a=x+y过A时a最大，即z最大，
由$\left\{\begin{array}{l}{x+3=2y}\\{y=2x}\end{array}\right.$得A（1，2）
所以${z}_{max}=（\sqrt{2}）^{1+2}=2\sqrt{2}$；
故答案为：2$\sqrt{2}$．

点评 本题考查了简单线性规划问题；关键是画出平面区域，利用目标函数的几何意义求最值．

练习册系列答案
相关题目
7．计算：${（0.027）^{-\frac{1}{3}}}-{log_3}2•{log_8}3$=3．
8．若向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足$\overrightarrow{a}+\overrightarrow{c}$=2$\overrightarrow{b}$，则称向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$依次成“等差”向量；若向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足$\overrightarrow{a}•\overrightarrow{c}$=$\overrightarrow{{b}^{2}}$，则称$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$依次成“等比”向量．已知直线l上不同三点A，B，C，O为直线l外一点，有以下说法：
①若$\overrightarrow{OA}，\overrightarrow{OB}，\overrightarrow{OC}$依次成“等差”向量，则点B是线段AC的中点；
②若点B是线段AC的中点，则$\overrightarrow{OA}，\overrightarrow{OB}，\overrightarrow{OC}$依次成“等差”向量；
③若点B是线段AC的中点，则$\overrightarrow{OA}，\overrightarrow{OB}，\overrightarrow{OC}$可能依次成“等比”向量；
④若|$\overrightarrow{OA}$|=5，|$\overrightarrow{OC}$|=8，|$\overrightarrow{AC}$|=7，则$\overrightarrow{OA}，\overrightarrow{OB}，\overrightarrow{OC}$不可能依次成“等比”向量．
其中说法正确的序号是①②④（把正确说法的序号都填上）
5．设正项等差数列{an}的前n项和为Sn，已知S5=40，且a4，a8-1，a15成等比数列，则S15等于（　　）
A．225B．345C．350D．535
12．在数列{an}，若a${\;}_{n}^{2}$-a${\;}_{n-1}^{2}$=k（n≥2，n∈N*，k为常数），则称{an}为等方差数列．
（1）若数列{bn}是等方差数列，b1=1，b2=3，写出所有满足条件的数列{bn}的前4项；
（2）若等方差数列{an}满足a1=2，a2=2$\sqrt{2}$，an＞0，设数列{$\frac{1}{{a}_{n}}$}的前n项和为Tn，是否存在正整数p，q，使不等式Tn＞$\sqrt{pn+q}$-1对一切n∈N*都成立？若存在，求出p，q的值；若不存在，说明理由．
2．函数f（x）=（$\frac{1}{5}$）${\;}^{{x}^{2}+ax}$在区间[1，2]上是单调减函数，则实数a的取值范围是（　　）
A．a≤-4B．a≤-2C．a≥-2D．a＞-4
9．已知函数f（x）=|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|．
（1）指出f（x）=|x+$\frac{1}{x}$|-|x-$\frac{1}{x}$|的基本性质（两条即可，结论不要求证明），并作出函数f（x）的图象；
（2）关于x的方程f2（x）+m|f（x）|+n=0（m，n∈R）恰有6个不同的实数解，求m的取值范围．
6．已知幂函数f（x）=（m-1）xa的图象过点（9，3），数列{an}各项均为正值，且a1=$\frac{m}{2}$，a2=m，且$\frac{{a}_{n}}{{a}_{n-1}}$=f（$\frac{{a}_{n+1}}{{a}_{n}}$）（n＞1），则a10=（　　）
A．210B．245C．288D．2511
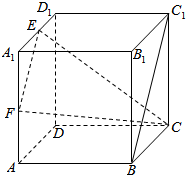7．如图，在棱长为1的正方体ABCD-A1B1C1D1中，E，F分别是A1D1，A1A的中点．
（1）求证：BC1∥平面CEF；
（2）在棱A1B1上是否存在点G，使得EG⊥CE？若存在，求A1G的长度；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网