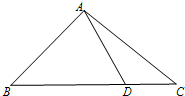
题目内容
在△ABC中,∠B=45°,b=
,cosC=
.
(1)求a;
(2)设AB的中点为D,求中线CD的长.
| 10 |
2
| ||
| 5 |
(1)求a;
(2)设AB的中点为D,求中线CD的长.
分析:(1)利用同角三角函数的关系和两角和的正弦公式,算出sinA=sin(B+C)=
,再正弦定理
=
的式子,即可解出a的长;
(2)利用余弦定理算出c=2.设CD=x,根据余弦定理关于三角形中线的定理建立关于x的方程,解得x=
,即得AB边的中线CD的长.
3
| ||
| 10 |
| a |
| sinA |
| b |
| sinB |
(2)利用余弦定理算出c=2.设CD=x,根据余弦定理关于三角形中线的定理建立关于x的方程,解得x=
| 13 |
解答:解:(1)∵cosC=
,∴sinC=
=
可得sinA=sin(B+C)=sinBcosC+cosBsinC=
•
+
•
=
由正弦定理
=
,得a=
=
=3
;
(2)∵由余弦定理,得c2=a2+b2-2abcosC
∴c2=18+10-2×3
×
×
=4,可得c=2
设中线CD=x,则有
∵AB2+(2CD)2=2(BC2+AC2),即c2+4x2=2(a2+b2)
∴4x2=2(a2+b2)-c2=2(18+10)-4=52,解之得x=
即AB边的中线CD的长等于
.
2
| ||
| 5 |
| 1-cos2C |
| ||
| 5 |

可得sinA=sin(B+C)=sinBcosC+cosBsinC=
| ||
| 2 |
2
| ||
| 5 |
| ||
| 2 |
| ||
| 5 |
3
| ||
| 10 |
由正弦定理
| a |
| sinA |
| b |
| sinB |
| bsinA |
| sinB |
| ||||||
|
| 2 |
(2)∵由余弦定理,得c2=a2+b2-2abcosC
∴c2=18+10-2×3
| 2 |
| 10 |
2
| ||
| 5 |
设中线CD=x,则有
∵AB2+(2CD)2=2(BC2+AC2),即c2+4x2=2(a2+b2)
∴4x2=2(a2+b2)-c2=2(18+10)-4=52,解之得x=
| 13 |
即AB边的中线CD的长等于
| 13 |
点评:本题给出三角形的两角和一条边,求一条边和一条中线的长.着重考查了同角三角函数关系、两角和的正弦公式和正余弦定理解三角形等知识,属于中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
在△ABC中,∠B=90°,AC=
,D,E两点分别在AB,AC上.使
=
=2,DE=3.将△ABC沿DE折成直二面角,则二面角A-EC-B的余弦值为( )
| 15 |
| 2 |
| AD |
| DB |
| AE |
| EC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,∠B=
,三边长a,b,c成等差数列,且a,
,c成等比数列,则b的值是( )
| π |
| 3 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|