题目内容
(本小题14分)
设函数![]() ,其中
,其中![]() .
.
(I)当![]() 时,判断函数
时,判断函数![]() 在定义域上的单调性;
在定义域上的单调性;
(II)求函数![]() 的极值点;
的极值点;
(III)证明对任意的正整数![]() ,不等式
,不等式![]() 都成立.
都成立.
(1)![]() 在定义域
在定义域![]() 上单调递增(2)见解析(3)见解析
上单调递增(2)见解析(3)见解析
解析:
(I) 函数![]() 的定义域为
的定义域为![]() . 1分
. 1分
![]() 2分
2分
令![]() ,则
,则![]() 在
在![]() 上递增,在
上递增,在![]() 上递减
上递减
![]() . 4分
. 4分
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上恒成立.
上恒成立.
![]() 即当
即当![]() 时,函数
时,函数![]() 在定义域
在定义域![]() 上单调递增. 5分
上单调递增. 5分
(II)分以下几种情形讨论:
(1)由(I)知当![]() 时函数
时函数![]() 无极值点. 6分
无极值点. 6分
(2)当![]() 时,
时,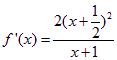
![]() 时,
时,![]()
![]() 时,
时,![]()
![]() 时,函数
时,函数![]() 在
在![]() 上无极值点. 7分
上无极值点. 7分
(3)当![]() 时,解
时,解![]() 得两个不同解
得两个不同解![]() ,
,![]() 8分
8分
当![]() 时,
时,![]() ,
,![]() ,
,
![]()
此时![]() 在
在![]() 上有唯一的极小值点
上有唯一的极小值点![]() . 9分
. 9分
当![]() 时,
时,![]()
![]() 在
在![]() 都大于0 ,
都大于0 ,![]() 在
在![]() 上小于0 ,
上小于0 ,
此时![]() 有一个极大值点
有一个极大值点![]() 和一个极小值点
和一个极小值点![]() .10分
.10分
综上可知,![]() 时,
时,![]() 在
在![]() 上有唯一的极小值点
上有唯一的极小值点![]() ;
;
![]() 时,
时,![]() 有一个极大值点
有一个极大值点![]() 和一个极小值点
和一个极小值点![]() ;
;
![]() 时,函数
时,函数![]() 在
在![]() 上无极值点.
上无极值点.
(III) 当![]() 时,
时,![]()
令![]() 则
则![]() 在
在![]() 上恒正
上恒正
![]() 在
在![]() 上单调递增
上单调递增
当![]() 时,恒有
时,恒有![]() . 12分
. 12分
即当![]() 时,有
时,有![]()
![]() ,
,
对任意正整数![]() ,取
,取![]() 得
得![]() 14分
14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
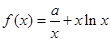 ,
, 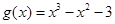 .
.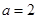 时,求曲线
时,求曲线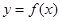 在
在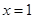 处的切线方程;
处的切线方程;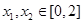 ,使得
,使得 成立,
成立,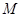 ;[来源:学。科。网Z。X。X。K]
;[来源:学。科。网Z。X。X。K]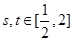 ,都有
,都有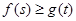 成立,求实数
成立,求实数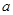 的取值范围.
的取值范围.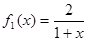 ,定义
,定义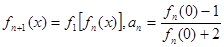 ,其中
,其中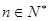 .
.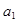 的值;
的值;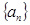 的通项公式;
的通项公式;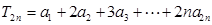 ,求
,求 的值.
的值.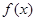 是定义在
是定义在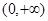 上的单调增函数,满足
上的单调增函数,满足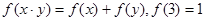 ,
,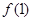 ; (2)若
; (2)若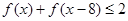 ,求
,求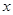 的取值范围。
的取值范围。