题目内容
(本小题14分)设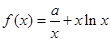 ,
, 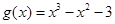 .
.
(1)当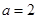 时,求曲线
时,求曲线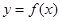 在
在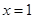 处的切线方程;
处的切线方程;
(2)如果存在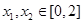 ,使得
,使得 成立,
成立,
求满足上述条件的最大整数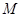 ;[来源:学。科。网Z。X。X。K]
;[来源:学。科。网Z。X。X。K]
(3)如果对任意的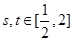 ,都有
,都有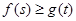 成立,求实数
成立,求实数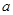 的取值范围.
的取值范围.
【答案】
(本小题14分)
(1)当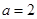 时,
时,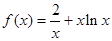 ,
,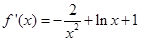 ,
, 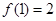 ,
, ,
,
所以曲线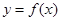 在
在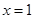 处的切线方程为
处的切线方程为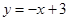 ;
(4分)
;
(4分)
(2)存在 ,使得
,使得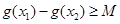 成立
成立
等价于: ,
,
考察 ,
,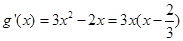 ,
,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
递减 |
极(最)小值 |
递增 |
|
 由上表可知:
由上表可知: ,
,
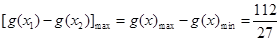 ,
,
所以满足条件的最大整数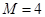 ;
(8分)
;
(8分)
(3)对任意的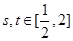 ,都有
,都有 成立
成立
等价于:在区间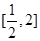 上,函数
上,函数 的最小值不小于
的最小值不小于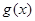 的最大值,
的最大值,
由(2)知,在区间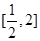 上,
上,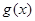 的最大值为
的最大值为 。
。
 ,下证当
,下证当 时,在区间
时,在区间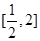 上,函数
上,函数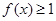 恒成立。
恒成立。
当 且
且 时,
时,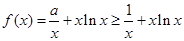 ,
,
记 ,
, ,
, 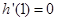 。
。
当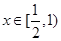 ,
,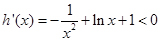 ;当
;当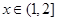 ,
,
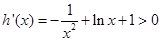 ,
,
所以函数 在区间
在区间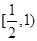 上递减,在区间
上递减,在区间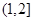 上递增,
上递增,
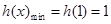 ,即
,即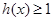 , 所以当
, 所以当 且
且 时,
时,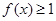 成立,
成立,
即对任意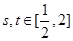 ,都有
,都有 。
(14分)
。
(14分)
(3)另解:当 时,
时,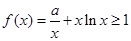 恒成立
恒成立
等价于 恒成立,
恒成立,
记 ,
,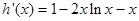 ,
, 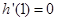 。
。
记 ,
,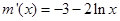 ,由于
,由于 ,
,
 ,
所以
,
所以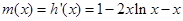 在
在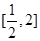 上递减,
上递减,
当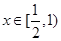 时,
时,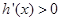 ,
,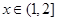 时,
时,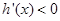 ,
,
即函数 在区间
在区间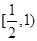 上递增,在区间
上递增,在区间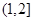 上递减,
上递减,
所以 ,所以
,所以 。
(14分)
。
(14分)
【解析】略

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目


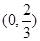
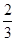
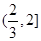

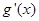

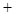
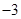
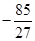
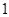
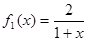 ,定义
,定义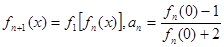 ,其中
,其中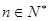 .
.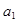 的值;
的值;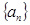 的通项公式;
的通项公式;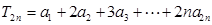 ,求
,求 的值.
的值.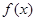 是定义在
是定义在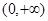 上的单调增函数,满足
上的单调增函数,满足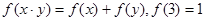 ,
,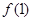 ; (2)若
; (2)若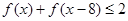 ,求
,求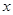 的取值范围。
的取值范围。