题目内容
已知命题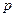 :“若
:“若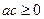 ,则二次方程
,则二次方程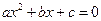 没有实根”.(1)写出命题
没有实根”.(1)写出命题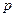 的否命题;(2)判断命题
的否命题;(2)判断命题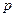 的否命题的真假,并证明你的结论.
的否命题的真假,并证明你的结论.
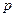 :“若
:“若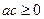 ,则二次方程
,则二次方程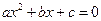 没有实根”.(1)写出命题
没有实根”.(1)写出命题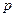 的否命题;(2)判断命题
的否命题;(2)判断命题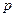 的否命题的真假,并证明你的结论.
的否命题的真假,并证明你的结论.(1)同解析;(2)命题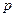 的否命题是真命题.
的否命题是真命题.
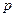 的否命题是真命题.
的否命题是真命题.(1)命题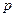 的否命题:“若
的否命题:“若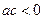 ,则二次方程
,则二次方程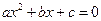 有实根”
有实根”
(2)命题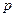 的否命题是真命题.证明如下:
的否命题是真命题.证明如下:
∵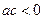 ,∴
,∴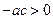 ,
,
∴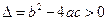 ,
,
二次方程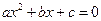 有实根,
有实根,
∴该命题是真命题.
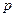 的否命题:“若
的否命题:“若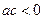 ,则二次方程
,则二次方程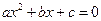 有实根”
有实根”(2)命题
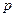 的否命题是真命题.证明如下:
的否命题是真命题.证明如下:∵
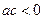 ,∴
,∴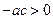 ,
,∴
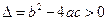 ,
,二次方程
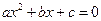 有实根,
有实根,∴该命题是真命题.

练习册系列答案
相关题目
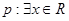 ,使得
,使得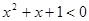 ,则
,则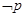 为:
为: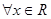 ,均有
,均有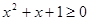
 ,则
,则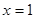 ”的逆否命题为“若
”的逆否命题为“若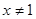 ,则
,则 ”
” 为假命题,则
为假命题,则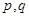 均为假命题
均为假命题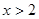 ”是“
”是“ ”的充分不必要条件
”的充分不必要条件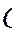 ◆■”中所有元素的个数为 ( )
◆■”中所有元素的个数为 ( ) 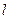 ⊥平面
⊥平面 ,直线
,直线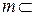 平面
平面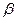 ,则下列命题:
,则下列命题: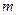 ,则
,则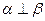 ;②若
;②若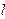 ⊥
⊥ 时,
时,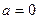 或
或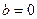 或
或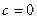 ”的逆命题、否命题、逆否命题,并判断其真假
”的逆命题、否命题、逆否命题,并判断其真假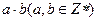 是偶数,那么a,b中至少有一个是偶数.”那么
是偶数,那么a,b中至少有一个是偶数.”那么
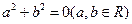 ,则
,则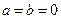 ”的逆否命题是( )
”的逆否命题是( )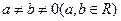 ,则
,则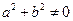
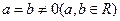 ,则
,则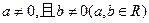 ,则
,则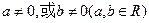 ,则
,则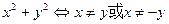
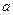 、
、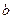 都是偶数,则
都是偶数,则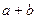 是偶数”的逆否命题是“若
是偶数”的逆否命题是“若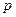 或
或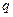 ”是假命题,则“非
”是假命题,则“非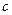 是实数,关于
是实数,关于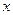 的不等式
的不等式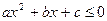 的解集是空集,必有
的解集是空集,必有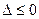
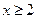 且
且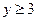 则
则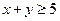 ”为假命题;③“
”为假命题;③“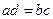 ”是“四个实数
”是“四个实数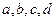 依次成等比数列”的必要而不充分条件. 其中不正确的命题序号是( )
依次成等比数列”的必要而不充分条件. 其中不正确的命题序号是( )