题目内容
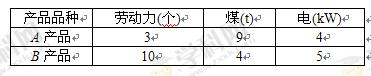
某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A原料1千克、B原料2千克;生产乙产品1桶需耗A原料2千克,B原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A、B原料都不超过12千克.求该公司从每天生产的甲、乙两种产品中,可获得的最大利润.
该公司从每天生产的甲、乙两种产品中,可获得的最大利润为2800元.
解析试题分析:设公司每天生产甲种产品x桶,乙种产品y桶,公司共可获得利润为z元/天,
则由已知,得z=300x+400y.
且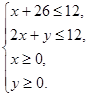
画可行域如图所示,
目标函数z=300x+400y可变形为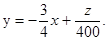
解方程组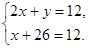 得,
得,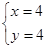 即A(4,4).
即A(4,4).
所以,Z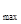 =1200+1600=2800.
=1200+1600=2800.
所以,该公司从每天生产的甲、乙两种产品中,可获得的最大利润为2800元. 9分
考点:简单线性规划的应用
点评:中档题,作为应用问题,解简单线性规划问题,要遵循“审清题意,设出变量,布列不等式组,画,移,解,答”等步骤。

练习册系列答案
相关题目
关于x的不等式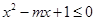 的解集中只有一个元素,则实数m =( ).
的解集中只有一个元素,则实数m =( ).
A.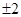 | B.2 | C.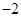 | D.不存在 |
函数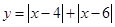 的最小值为( )
的最小值为( )
| A.2 | B. | C.4 | D.6 |
已知不等式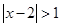 的解集与不等式
的解集与不等式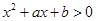 的解集相同,则
的解集相同,则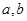 的值为( )
的值为( )
A.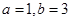 | B.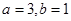 |
C.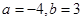 | D.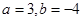 |
已知a+b>0,b<0,那么a,b,-a,-b的大小关系是( )
| A.a>b>-b>-a | B.a>-b>-a>b |
| C.a>-b>b>-a | D.a>b>-a>-b |
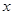 的二次函数
的二次函数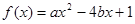 .
.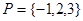 和
和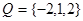 ,分别从集合P和Q中随机取一个数作为
,分别从集合P和Q中随机取一个数作为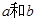 ,求函数
,求函数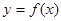 在区间
在区间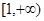 上是增函数的概率;
上是增函数的概率;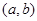 是区域
是区域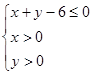 内的随机点,求函数
内的随机点,求函数 在区间
在区间 ,
,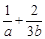 的最小值.
的最小值. 的实数
的实数 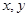 ,不等式
,不等式 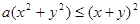 恒成立,则实数
恒成立,则实数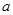 的最大值是_______.
的最大值是_______.