题目内容
【题目】已知函数
且
的导函数为
。
（1）求函数的极大值；
（2）若函数有两个零点
，求a的取值范围。
（3）在（2）的条件下，求证：
【答案】(1) 
；(2)
；(3)详见解析.
【解析】
（1）求函数导数，分析函数的单调性，进而可得极大值；
（2）结合（1）中的单调性可得
，进而利用零点存在定理可说明有两个零点；
（3）不妨设
,结合条件可得
，构造
，求函数导数分析单调性即可证得.
解：
因为
，所以
，
当
时，
，
在
单调递增
当
时，
，在
单调递减
所以当时，有极大值
.
当时，由知在单调递增，在单调递减，有极大值，故若有两个零点，则必有
令
，则
在单调递增，所以
，
所以
，则当
时，
，又
所以在和各有一个零点，所以
的取值范围为
不妨设,则
，
.
.
所以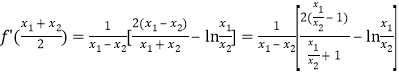
令
所以
单调递减
，所以
练习册系列答案
相关题目
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度，现在某市进行调查，随机调查了
人，他们年龄的频数分布及支持“生育二胎”人数如下表：
年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生 育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
（1）由以上统计数据填下面2乘2列联表，并问是否有99
的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异：
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
支持 | a= | c= | |
不支持 | b= | d= | |
合计 |
（2）若对年龄在
的被调查人中随机选取两人进行调查，恰好这两人都支持“生育二胎放开”的概率是多少？
参考数据：P
