题目内容
本小题共13分)
若数列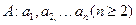 满足
满足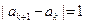
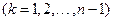 ,则称
,则称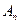 为
为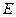 数列。记
数列。记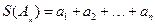 。
。
(Ⅰ)写出一个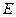 数列
数列 满足
满足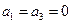 ;
;
(Ⅱ)若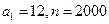 ,证明:
,证明: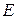 数列
数列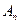 是递增数列的充要条件是
是递增数列的充要条件是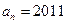 ;
;
(Ⅲ)在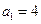 的
的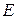 数列
数列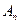 中,求使得
中,求使得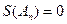 成立的
成立的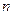 的最小值。
的最小值。
略
解析

练习册系列答案
相关题目
题目内容
本小题共13分)
若数列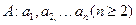 满足
满足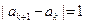
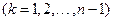 ,则称
,则称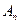 为
为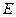 数列。记
数列。记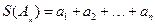 。
。
(Ⅰ)写出一个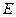 数列
数列 满足
满足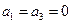 ;
;
(Ⅱ)若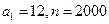 ,证明:
,证明: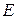 数列
数列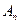 是递增数列的充要条件是
是递增数列的充要条件是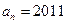 ;
;
(Ⅲ)在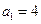 的
的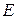 数列
数列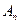 中,求使得
中,求使得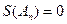 成立的
成立的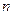 的最小值。
的最小值。
略
解析
