题目内容
问题:过点M(2,1)作一斜率为1的直线交抛物线y2=2px(p>0)于不同的两点A,B,且点M为AB的中点,求p的值.请阅读某同学的问题解答过程:解:设A(x1,y1),B(x2,y2),则y12=2px1,y22=2px2,两式相减,得(y1-y2)(y1+y2)=2p(x1-x2).又
 ,y1+y2=2,因此p=1.
,y1+y2=2,因此p=1.并给出当点M的坐标改为(2,m)(m>0)时,你认为正确的结论: .
【答案】分析:设A(x1,y1),B(x2,y2),则y12=2px1,y22=2px2,两式相减,得(y1-y2)(y1+y2)=2p(x1-x2).又 ,y1+y2=2m所以p=m,将直线方程与抛物线的方程联立,判别式大于0求出m的范围.
,y1+y2=2m所以p=m,将直线方程与抛物线的方程联立,判别式大于0求出m的范围.
解答:解:设A(x1,y1),B(x2,y2),
则y12=2px1,y22=2px2,
两式相减,得(y1-y2)(y1+y2)=2p(x1-x2).
又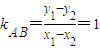 ,y1+y2=2m
,y1+y2=2m
所以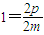
所以p=m
因为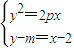 消去x得
消去x得
y2-2py+2pm-4p=0
即y2-2my+2m2-4m=0
△=4m2-4(2m2-4m)>0
解得0<m<4
故答案为:p=m(0<m<4)
点评:解决直线与圆锥曲线相交有关弦中点的问题,常利用点差法来解决,但注意需要将直线的方程与圆锥曲线的方程联立,判别式大于0.
 ,y1+y2=2m所以p=m,将直线方程与抛物线的方程联立,判别式大于0求出m的范围.
,y1+y2=2m所以p=m,将直线方程与抛物线的方程联立,判别式大于0求出m的范围.解答:解:设A(x1,y1),B(x2,y2),
则y12=2px1,y22=2px2,
两式相减,得(y1-y2)(y1+y2)=2p(x1-x2).
又
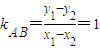 ,y1+y2=2m
,y1+y2=2m所以
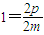
所以p=m
因为
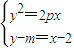 消去x得
消去x得y2-2py+2pm-4p=0
即y2-2my+2m2-4m=0
△=4m2-4(2m2-4m)>0
解得0<m<4
故答案为:p=m(0<m<4)
点评:解决直线与圆锥曲线相交有关弦中点的问题,常利用点差法来解决,但注意需要将直线的方程与圆锥曲线的方程联立,判别式大于0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
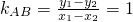 ,y1+y2=2,因此p=1.
,y1+y2=2,因此p=1.