题目内容
定义函数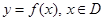 ,若存在常数C,对任意的
,若存在常数C,对任意的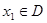 ,存在唯一的
,存在唯一的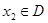 ,使得
,使得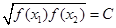 ,则称函数
,则称函数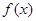 在D上的几何平均数为C.已知
在D上的几何平均数为C.已知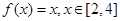 ,则函数
,则函数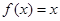 在
在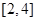 上的几何平均数为( )
上的几何平均数为( )
A.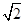 B.
B.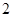 C.
C.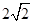 D.
D.
C
解析试题分析:根据已知中关于函数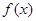 在D上的几何平均数为C的定义,结合
在D上的几何平均数为C的定义,结合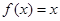 在区间[2,4]单调递增,则
在区间[2,4]单调递增,则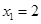 时,存在唯一的
时,存在唯一的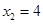 与之对应,故
与之对应,故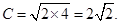
考点:本小题主要考查函数的单调性性质的应用.
点评:本题考查的知识点是函数单调性的性质,其中根据函数在区间上的几何平均数的定义,判断出C等于函数在区间D上最大值与最小值的几何平均数,是解答本题的关键

练习册系列答案
相关题目
方程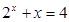 的根所在区间为 ( )
的根所在区间为 ( )
A.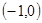 | B.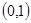 | C.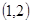 | D.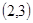 |
若函数f (x) = x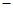
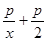 在[1,+∞)上是增函数,则实数p的取值范围是( )
在[1,+∞)上是增函数,则实数p的取值范围是( )
A.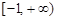 | B.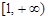 | C.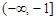 | D.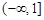 |
设偶函数f(x)的定义域为R,当x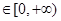 时f(x)是增函数,则f(-2),f(
时f(x)是增函数,则f(-2),f( ),f(-3)的大小关系是:( )
),f(-3)的大小关系是:( )
A.f( )>f(-3)>f(-2) )>f(-3)>f(-2) | B.f( )>f(-2)>f(-3) )>f(-2)>f(-3) |
C.f( )<f(-3)<f(-2) )<f(-3)<f(-2) | D.f( )<f(-2)<f(-3) )<f(-2)<f(-3) |
函数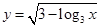 的定义域为( )
的定义域为( )
A.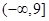 | B.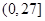 | C. | D.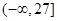 |
下列各组函数中表示同一函数的是 ( )
A.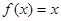 与 与 |
B.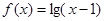 与 与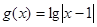 |
C.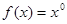 与 与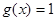 |
D.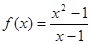 与 与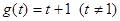 |
下列函数中,既是偶函数,又在区间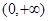 上单调递减的是( )
上单调递减的是( )
A.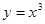 | B.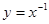 | C.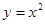 | D.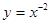 |
已知函数f(x)是R上的增函数,A(0,-2),B(3,2)是其图象上的两点,那么|f(x+1)|<2的解集是( )
| A.(1,4) | B.(-1,2) |
| C.(-∞,1)∪[4,+∞) | D.(-∞,-1)∪[2,+∞) |
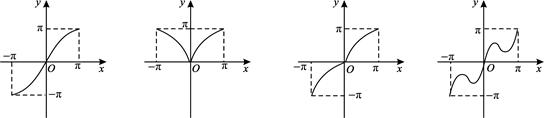
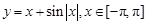 ,的大致图象是
,的大致图象是