题目内容
 如图,三棱锥D-ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC.
如图,三棱锥D-ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC.
(Ⅰ) 求证:平面CDE⊥平面ABD;
(Ⅱ) 求直线AD和平面CDE所成的角的大小;
(Ⅲ) 求点A到平面BCD的距离.
解:(Ⅰ)∵AD⊥平面ABC,CE?平面ABC∴AD⊥CE,
又∵△ABC为正三角形,E为AB的中点,
∴CE⊥AB而AB∩AD=A
∴CE⊥平面ABD,又CE?平面CDE
∴平面CDE⊥平面ABD
(Ⅱ)由(Ⅰ)得平面CDE⊥平面ABD,
∴AD在平面CDE上的射影为DE,所以∠ADE即为所成的角.
△ADE为Rt△,且AE=2,AD=3,∴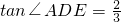 ∴
∴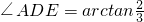 ,即直线AD与平面CDE所成的角为
,即直线AD与平面CDE所成的角为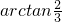
(Ⅲ)取BC的中点M,连接DM,过A点在平面DAM内作AN⊥DM于N
证得BC⊥平面DAM,所以AM⊥平面BCD
AM= ,DM=
,DM= ,
,
利用等面积可知,DM•AN=DA•AM
所以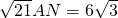
∴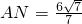
分析:(Ⅰ)根据AD⊥平面ABC,可得AD⊥CE,又△ABC为正三角形,E为AB的中点,可知CE⊥AB,从而CE⊥平面ABD,故可得平面CDE⊥平面ABD;
(Ⅱ)由(Ⅰ)得平面CDE⊥平面ABD,所以AD在平面CDE上的射影为DE,故∠ADE即为所成的角,在Rt△ADE中,AE=2,AD=3,故可求直线AD与平面CDE所成的角;
(Ⅲ)取BC的中点M,连接DM,过A点在平面DAM内作AN⊥DM于N,可证得BC⊥平面DAM,所以AM⊥平面BCD,利用DM•AN=DA•AM
可求点A到平面BCD的距离.
点评:本题以三棱锥为载体,考查线面垂直的性质,考查面面垂直,考查线面角,考查点面距离,综合性强.
又∵△ABC为正三角形,E为AB的中点,
∴CE⊥AB而AB∩AD=A
∴CE⊥平面ABD,又CE?平面CDE
∴平面CDE⊥平面ABD
(Ⅱ)由(Ⅰ)得平面CDE⊥平面ABD,
∴AD在平面CDE上的射影为DE,所以∠ADE即为所成的角.
△ADE为Rt△,且AE=2,AD=3,∴
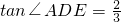 ∴
∴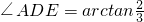 ,即直线AD与平面CDE所成的角为
,即直线AD与平面CDE所成的角为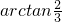
(Ⅲ)取BC的中点M,连接DM,过A点在平面DAM内作AN⊥DM于N
证得BC⊥平面DAM,所以AM⊥平面BCD
AM=
 ,DM=
,DM= ,
,利用等面积可知,DM•AN=DA•AM
所以
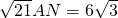
∴
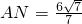
分析:(Ⅰ)根据AD⊥平面ABC,可得AD⊥CE,又△ABC为正三角形,E为AB的中点,可知CE⊥AB,从而CE⊥平面ABD,故可得平面CDE⊥平面ABD;
(Ⅱ)由(Ⅰ)得平面CDE⊥平面ABD,所以AD在平面CDE上的射影为DE,故∠ADE即为所成的角,在Rt△ADE中,AE=2,AD=3,故可求直线AD与平面CDE所成的角;
(Ⅲ)取BC的中点M,连接DM,过A点在平面DAM内作AN⊥DM于N,可证得BC⊥平面DAM,所以AM⊥平面BCD,利用DM•AN=DA•AM
可求点A到平面BCD的距离.
点评:本题以三棱锥为载体,考查线面垂直的性质,考查面面垂直,考查线面角,考查点面距离,综合性强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
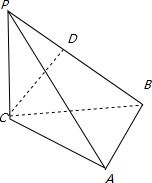 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB. 如图,三棱锥D-ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC.
如图,三棱锥D-ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC.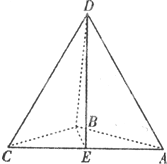 如图,三棱锥D-ABC中,AB,BC,BD两两垂直,且AB=BC=2,点E是AC中点,异面直线AD与BE所成角为θ.
如图,三棱锥D-ABC中,AB,BC,BD两两垂直,且AB=BC=2,点E是AC中点,异面直线AD与BE所成角为θ.