题目内容
 (A题)如图正方体ABCD-A1B1C1D1,则下列四个命题:
(A题)如图正方体ABCD-A1B1C1D1,则下列四个命题:
①P在直线BC1上运动时,三棱锥A-D1PC的体积不变;
②P在直线BC1上运动时,二面角P-AD1-C的大小不变;
③P在直线BC1上运动时,直线AP与平面ACD1所成角的大小不变;
④M是平面A1B1C1D1上到点D和C1距离相等的点,则M点必在直线A1D1上其中真命题的编号是________(写出所有真命题的编号).
①②④
分析:①利用线面平行的性质和三棱锥的体积计算公式即可得出;
②利用二面角的定义即可得出;
③利用①的结论及线面角的定义即可判断出;
④通过建立空间直角坐标系,利用两点间的距离公式即可得出.
解答:①∵BC1∥AD1,BC1?平面ACD1,而AD1?平面ACD1,∴BC1∥平面ACD1.因此P在直线BC1上运动时,点P到平面ACD1的距离不变,三棱锥P-ACD1即A-D1PC的体积不变,正确;
②P在直线BC1上运动时,二面角BC1-AD1-C大小不变,即二面角P-AD1-C的大小不变,正确;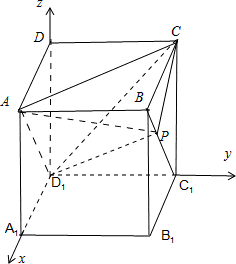
③由①可知:P在直线BC1上运动时,点P到平面ACD1的距离h不变,而AP随着点P的变化而变化,设AP与平面ACD1所成的角为θ,
则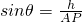 随着AP的改变而改变,因此不正确;
随着AP的改变而改变,因此不正确;
④距离如图所示的空间直角坐标系,设M(x,y,0),不妨设D1A1=1,则C1(0,1,0),D(0,0,1).
∵|MD|=|MC1|,∴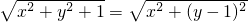 ,解得y=0.
,解得y=0.
∴点M(x,0,0).
则M点必在直线A1D1上.因此正确.
综上可知:正确命题是①②④.
故答案为①②④.
点评:熟练掌握线面平行的性质和三棱锥的体积计算公式、二面角的定义、线面角的定义、建立空间直角坐标系、两点间的距离公式是解题的关键.
分析:①利用线面平行的性质和三棱锥的体积计算公式即可得出;
②利用二面角的定义即可得出;
③利用①的结论及线面角的定义即可判断出;
④通过建立空间直角坐标系,利用两点间的距离公式即可得出.
解答:①∵BC1∥AD1,BC1?平面ACD1,而AD1?平面ACD1,∴BC1∥平面ACD1.因此P在直线BC1上运动时,点P到平面ACD1的距离不变,三棱锥P-ACD1即A-D1PC的体积不变,正确;
②P在直线BC1上运动时,二面角BC1-AD1-C大小不变,即二面角P-AD1-C的大小不变,正确;

③由①可知:P在直线BC1上运动时,点P到平面ACD1的距离h不变,而AP随着点P的变化而变化,设AP与平面ACD1所成的角为θ,
则
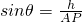 随着AP的改变而改变,因此不正确;
随着AP的改变而改变,因此不正确;④距离如图所示的空间直角坐标系,设M(x,y,0),不妨设D1A1=1,则C1(0,1,0),D(0,0,1).
∵|MD|=|MC1|,∴
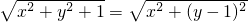 ,解得y=0.
,解得y=0.∴点M(x,0,0).
则M点必在直线A1D1上.因此正确.
综上可知:正确命题是①②④.
故答案为①②④.
点评:熟练掌握线面平行的性质和三棱锥的体积计算公式、二面角的定义、线面角的定义、建立空间直角坐标系、两点间的距离公式是解题的关键.

练习册系列答案
相关题目
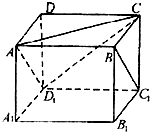 (A题)如图正方体ABCD-A1B1C1D1,则下列四个命题:
(A题)如图正方体ABCD-A1B1C1D1,则下列四个命题:

 (本小题满分8分)设蚂蚁在如图正方体的表面沿棱爬行,它从一个顶点爬向另外三个顶点是等可能的,若蚂蚁的初始位置在顶点A,回答下列问题:
(本小题满分8分)设蚂蚁在如图正方体的表面沿棱爬行,它从一个顶点爬向另外三个顶点是等可能的,若蚂蚁的初始位置在顶点A,回答下列问题: